
(2)已知![]() ,求
,求![]() 的值.
的值.
(3)已知方程sin(α-3π)=2cos(α-4π),求 的值.
的值.
(4)已知tan(π-α)=a2,|cos(π-α)|=-cosα,求![]() 的值.
的值.
思路分析:考查誘導公式和同角三角函數關系式的應用.前三個可以利用誘導公式和同角三角函數關系式將條件和所求的式子化簡.而(4)除了化簡之外,還應判斷角終邊的位置.
解:(1)∵sin(3π+α)=sin(π+α)=-sinα,∴sinα=![]() .
.
∴原式=![]() .
.
(2)![]() .
.
(3)∵sin(α-3π)=2cos(α-4π),
∴-sin(3π-α)=2cos(4π-α).
∴-sin(π-α)=2cos(-α).
∴sinα=-2cosα,且cosα≠0.
∴原式=![]() .
.
(4)由題設,tanα=-a2≤0,|cosα|=-cosα,即cosα≤0.
由此,當a≠0時,tanα<0,cosα<0,α為第二象限角,
∴原式=![]() .
.
當a=0時,tanα=0,α=kπ,∴cosα=±1.
∵cosα≤0,∴cosα=-1.
∴原式=![]() (a=0).
(a=0).
綜上所述:![]() .
.
方法歸納 三角函數中角的變換是個難點,三角函數中的許多問題正是通過挖掘角與角之間的內在聯系而解決的.而化簡求值要遵循“負化正,大化小”的原則.
深化升華 本題是一個化簡求值的題型,它的特點是已知一個復雜的等式,求另一個復雜的式子的值.解決這類問題的策略是:化簡,化簡,再化簡.


科目:高中數學 來源: 題型:
| 3 |
| π |
| 2 |
| 3π |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |
| π |
| 2 |
| ||
| 5 |
| π |
| 2 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2010-2011年浙江省高一下學期第一次質量檢測數學試卷 題型:解答題
(1)已知sin(3π-α)=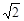 cos(
cos( +β),
+β),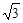 cos(-α)=-
cos(-α)=-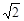 cos(π+β),
cos(π+β),
且0<α<π, 0<β<π,求α, cosβ.
(2)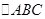 中,
中,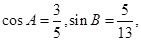 求
求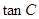
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com