分析:(1)利用線面垂直的判定定理,證明B1D1⊥平面AA1C1,利用面面垂直的判定,可得平面AB1D1⊥平面AA1C1;
(2)過點B1作B1H⊥AC1于H,連接D1H,則D1H⊥AC1,先確定正四棱柱ABCD-A1B1C1D1是棱長為1的正方體,再求四棱錐A-A1B1C1D1的體積
解答:(1)證明:∵AA
1⊥平面A
1B
1C
1D
1,B
1D
1?平面A
1B
1C
1D
1,
∴AA
1⊥B
1D
1,
∵B
1D
1⊥A
1C
1,AA
1∩A
1C
1=A
1,
∴B
1D
1⊥平面AA
1C
1,
∵B
1D
1?平面AB
1D
1,
∴平面AB
1D
1⊥平面AA
1C
1;
(2)解:過點B
1作B
1H⊥AC
1于H,連接D
1H,則D
1H⊥AC
1,B
1H=D
1H,∴∠B
1HD
1=120°
在△B
1HD
1中,由余弦定理可得
B1D12=
B1H2+D1H2-2B1H×D1H×cos120°=2
∴B
1H=D
1H=
,
在Rt△AB
1C
1中,由等面積可得AB
1×B
1C
1=B
1H×AC
1即
×1=×∴h=1,
此時,正四棱柱ABCD-A
1B
1C
1D
1是棱長為1的正方體,四棱錐A-A
1B
1C
1D
1的體積為
V=×1×1=.
點評:本題考查線面垂直、面面垂直的判定,考查四棱錐體積的計算,考查學生分析解決問題的能力,掌握線面垂直、面面垂直的判定定理是關鍵.

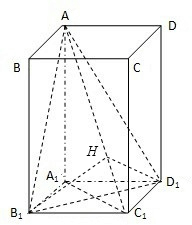
 (2012•汕頭二模)如圖,已知ABCD-A1B1C1D1是底面邊長為1的正四棱柱,
(2012•汕頭二模)如圖,已知ABCD-A1B1C1D1是底面邊長為1的正四棱柱,


 核心素養學練評系列答案
核心素養學練評系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案