
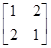 ���£�
���£�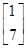 ��Ӌ��M5��.
��Ӌ��M5��. ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
 (k��0)��һ���������������
(k��0)��һ��������������� ��A������A��1����(y��ng)��׃�Q���c(3��1)׃?y��u)��c(1��1)����(sh��)a��k��ֵ��
��A������A��1����(y��ng)��׃�Q���c(3��1)׃?y��u)��c(1��1)����(sh��)a��k��ֵ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
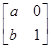 (a>0)����(y��ng)��׃�Q�����µõ���������x2��y2��1.
(a>0)����(y��ng)��׃�Q�����µõ���������x2��y2��1.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
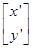 ��
��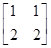
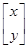 �£�ֱ��x��y��k(k�鳣��(sh��))�ϵ������c��׃?y��u)�һ���c������c����(bi��o)��
�£�ֱ��x��y��k(k�鳣��(sh��))�ϵ������c��׃?y��u)�һ���c������c����(bi��o)���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
 .
.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
| . |
| z |
| A��5 | B��6 | C��
| D��4 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
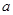 ��
��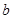 ��
��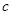 ��
��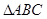 ����߅�L���ҝM��
����߅�L���ҝM��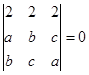 ���t
���t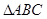 һ���ǣ� ����
һ���ǣ� ���� | A�������ǵ�߅������ | B����߅������ |
| C��ֱ�������� | D������ֱ�������� |
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com