
生產A,B兩種元件,其質量按測試指標劃分為:指標大于或等于82為正品,小于82為次品.現隨機抽取這兩種元件各100件進行檢測,檢測結果統計如下:
| 測試指標 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(I)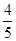 ,
,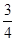 ;(II)(i)分布列見解析,
;(II)(i)分布列見解析,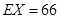 ;(ii)
;(ii)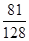 .
.
解析試題分析:(I)用指標大于或等于82所對應的的元件的個數除以總的元件個數即是正品的概率;(II)(i)根據題意分別求出一件A正品和一件B正品,一件A次品和一件B正品,一件A正品和一件B次品,一件A次品和一件B次品的概率,列出分布列,由公式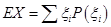 求出數學期望;(ii)根據題意設出5件元件中正品和次品的數量,列不等式
求出數學期望;(ii)根據題意設出5件元件中正品和次品的數量,列不等式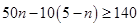 求解,根據解得的
求解,根據解得的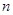 的值求解概率.
的值求解概率.
試題解析:(I)元件 為正品的概率約為
為正品的概率約為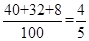 . 1分
. 1分
元件 為正品的概率約為
為正品的概率約為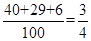 . 2分
. 2分
(II)(i)隨機變量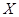 的所有取值為
的所有取值為 . 3分
. 3分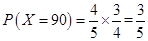 ;
; 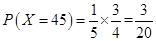 ;
;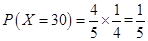 ;
; 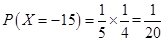 . 7分
. 7分
所以,隨機變量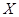 的分布列為:
的分布列為:
8分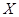
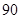
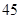
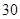
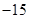
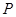
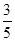
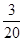
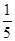
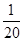
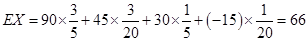 . 9分
. 9分
(ii)設生產的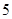 件元件
件元件 中正品有
中正品有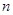 件,則次品有
件,則次品有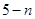 件.
件.
依題意,得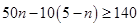 , 解得
, 解得 .
.
∴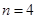 或
或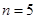 . 10分
. 10分
設“生產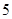 件元件
件元件 所獲得的利潤不少于
所獲得的利潤不少于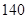 元”為事件
元”為事件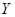 ,
,
則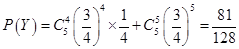 . 12分
. 12分
考點:1、隨機事件的概率;2、求離散型隨機變量的分布列和數學期望;3、解不等式.


 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:解答題
設進入某商場的每一位顧客購買甲種商品的概率為0.5,購買乙種商品的概率為0.6, 且購買甲種商品與購買乙種商品相互獨立,各顧客之間購買商品也是相互獨立的.
(1)求進入商場的1位顧客至少購買甲、乙兩種商品中的一種的概率;
(2)記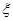 表示進入商場的3位顧客中至少購買甲、乙兩種商品中的一種的人數,求
表示進入商場的3位顧客中至少購買甲、乙兩種商品中的一種的人數,求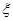 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市為增強市民的環境保護意識,面向全市征召義務宣傳志愿者.把符合條件的1000名志愿者按年齡分組:第1組[20,25)、第2組[25,30)、第3組[30,35)、第4組[35,40)、第5組[40,45],得到的頻率分布直方圖如圖所示: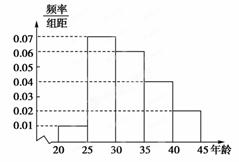
(1)若從第3、4、5組中用分層抽樣的方法抽取12名志愿者參加廣場的宣傳活動,應從第3、4、5組各抽取多少名志愿者?
(2)在(1)的條件下,該市決定在這12名志愿者中隨機抽取3名志愿者介紹宣傳經驗,求第4組至少有一名志愿者被抽中的概率;
(3)在(2)的條件下,若ξ表示抽出的3名志愿者中第3組的人數,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某食品企業一個月內被消費者投訴的次數用 表示,椐統計,隨機變量
表示,椐統計,隨機變量 的概率分布如下:
的概率分布如下:
 | 0 | 1 | 2 | 3 |
| p | 0.1 | 0.3 | 2a | a |
 的數學期望;
的數學期望;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
小波以游戲方式決定參加學校合唱團還是參加學校排球隊.游戲規則為:以O為起點,再從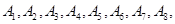 (如圖)這8個點中任取兩點分別為終點得到兩個向量,記這兩個向量的數量積為
(如圖)這8個點中任取兩點分別為終點得到兩個向量,記這兩個向量的數量積為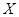 .若
.若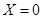 就參加學校合唱團,否則就參加學校排球隊.
就參加學校合唱團,否則就參加學校排球隊.
(I)求小波參加學校合唱團的概率;
(II)求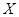 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品按質量標準分為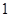 ,
, ,
,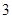 ,
,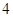 ,
,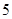 五個等級.現從一批該產品隨機抽取20個,對其等級進行統計分析,得到頻率分布表如下:
五個等級.現從一批該產品隨機抽取20個,對其等級進行統計分析,得到頻率分布表如下:
| 等級 | 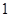 |  | 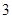 | 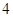 | 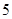 |
| 頻率 | 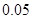 | 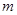 | 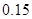 | 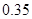 | 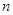 |
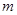 ,
,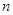 ;
;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某品牌汽車的4 店,對最近100位采用分期付款的購車者進行了統計,統計結果如下表所示:已知分3期付款的頻率為0.2,且4
店,對最近100位采用分期付款的購車者進行了統計,統計結果如下表所示:已知分3期付款的頻率為0.2,且4 店經銷一輛該品牌的汽車,顧客若一次付款,其利潤為1萬元;若分2期付款或3期付款,其利潤為1.5萬元;若分4期付款或5期付款,其利潤為2萬元.用
店經銷一輛該品牌的汽車,顧客若一次付款,其利潤為1萬元;若分2期付款或3期付款,其利潤為1.5萬元;若分4期付款或5期付款,其利潤為2萬元.用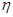 表示經銷一輛該品牌汽車的利潤.
表示經銷一輛該品牌汽車的利潤.
| 付款方式 | 一次 | 分2期 | 分3期 | 分4期 | 分5期 |
| 頻數 | 40 | 20 | a | 10 | b |
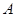 :“購買該品牌汽車的3位顧客中,至多有1位采用分3期付款”的概率
:“購買該品牌汽車的3位顧客中,至多有1位采用分3期付款”的概率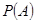 ;
;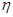 的分布列及其數學期望
的分布列及其數學期望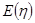 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了比較“傳統式教學法”與我校所創立的“三步式教學法”的教學效果.共選100名學生隨機分成兩個班,每班50名學生,其中一班采取“傳統式教學法”,二班實行“三步式教學法”
(Ⅰ)若全校共有學生2000名,其中男生1100名,現抽取100名學生對兩種教學方式的受歡迎程度進行問卷調查,應抽取多少名女生?
(Ⅱ)下表1,2分別為實行“傳統式教學”與“三步式教學”后的數學成績:
表1
| 數學成績 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 頻 數 | 15 | 20 | 10 | 5 |
| 數學成績 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 頻 數 | 5 | 40 | 3 | 2 |
| 班 次 | 120分以下(人數) | 120分以上(人數) | 合計(人數) |
| 一班 | | | |
| 二班 | | | |
| 合計 | | | |
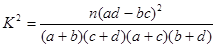 ,其中
,其中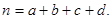
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了調査某大學學生在某天上網的時間,隨機對lOO名男生和100名女生進行了不記名的問卷調查.得到了如下的統計結果:
表l:男生上網時間與頻數分布表
表2:女生上網時間與頻數分布表
(I)從這100名男生中任意選出3人,其中恰有1人上網時間少于60分鐘的概率;
(II)完成下面的2X2列聯表,并回答能否有90%的把握認為“大學生上網時間與性別有關”?
表3: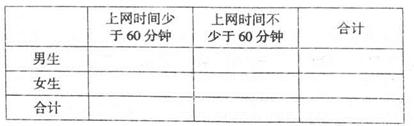 •
•
附: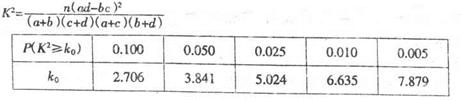
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com