
設函數 .
.
若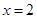 是函數
是函數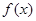 的極值點,1和
的極值點,1和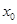 是函數
是函數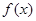 的兩個不同零點,且
的兩個不同零點,且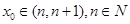 ,求
,求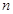 .
.
若對任意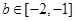 ,都存在
,都存在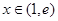 (
(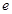 為自然對數的底數),使得
為自然對數的底數),使得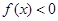 成立,求實數
成立,求實數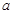 的取值范圍.
的取值范圍.
(1)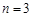 ;(2)
;(2)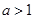 .
.
【解析】
試題分析:(1)對零點存在性定理的考查,借助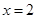 是極值及1是零點建立兩個方程解出
是極值及1是零點建立兩個方程解出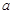 和
和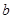 ,然后對函數
,然后對函數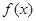 進行求導定出其單調性,再利用零點存在性定理嘗試算出
進行求導定出其單調性,再利用零點存在性定理嘗試算出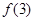 和
和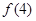 ,發現異號,得出零點所在的區間;(2)首先需要我們將兩個變量的不等式恒成立問題轉化成常見的一個變量的不等式有解問題,然后再構造這個不等式為函數
,發現異號,得出零點所在的區間;(2)首先需要我們將兩個變量的不等式恒成立問題轉化成常見的一個變量的不等式有解問題,然后再構造這個不等式為函數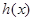 ,為了找
,為了找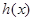 的最小值并且讓其小于0,我們利用試根法試出
的最小值并且讓其小于0,我們利用試根法試出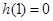 ,然后只要讓
,然后只要讓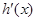 右零點在端點1右邊即可,解出范圍.
右零點在端點1右邊即可,解出范圍.
試題解析:(1)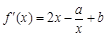 ,∵
,∵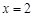 是函數
是函數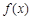 的極值點,∴
的極值點,∴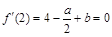 .∵1是函數
.∵1是函數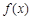 的零點,得
的零點,得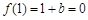 ,由
,由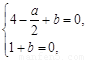 解得
解得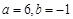 . ∴
. ∴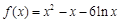 ,
,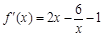 ,
,
令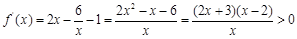 ,
,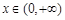 ,得
,得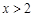 ; 令
; 令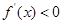 得
得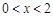 ,所以
,所以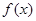 在
在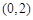 上單調遞減;在
上單調遞減;在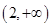 上單調遞增.故函數
上單調遞增.故函數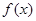 至多有兩個零點,其中
至多有兩個零點,其中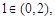
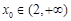 ,因為
,因為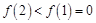 ,
,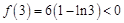 ,
,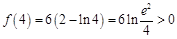 ,所以
,所以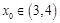 ,故
,故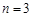 .
.
(2)令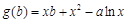 ,
,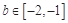 ,則
,則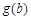 為關于
為關于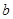 的一次函數且為增函數,根據題意,對任意
的一次函數且為增函數,根據題意,對任意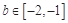 ,都存在
,都存在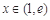 ,使得
,使得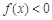 成立,則
成立,則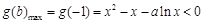 在
在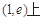 有解,令
有解,令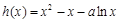 ,只需存在
,只需存在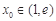 使得
使得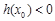 即可,
即可,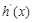 =
=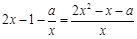 ,令
,令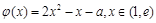 ,∵
,∵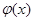 的兩個零點分布在
的兩個零點分布在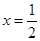 左右,又∵
左右,又∵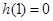 ,∴
,∴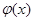 的右零點必須大于1,∴
的右零點必須大于1,∴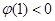 ,解得
,解得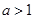 .綜上所述,當
.綜上所述,當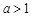 時,對任意
時,對任意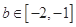 ,都存在
,都存在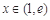 ,使得
,使得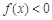 成立.
成立.
考點:1.零點存在性定理;2.根的分布.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
| 3x-1 |
| x+1 |
| 1 |
| 2 |
| t-1 |
| t |
| s+1 |
| s |
| s+1 |
| s |
| t-1 |
| t |
| 11 |
| 17 |
| 1 |
| xn-1 |
查看答案和解析>>
科目:高中數學 來源:2014屆浙江臺州高二下學期第一次月考理科數學試卷(解析版) 題型:解答題
設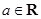 ,函數
,函數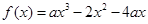 ,
,
(1)若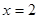 是函數
是函數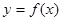 的極值點,求
的極值點,求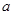 的值;
的值;
(2)在(1)的條件下,求函數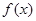 在區間
在區間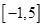 上的最值.
上的最值.
(3)是否存在實數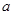 ,使得函數
,使得函數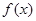 在
在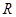 上為單調函數,若是,求出
上為單調函數,若是,求出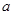 的取值范圍,若不是,請說明理由。
的取值范圍,若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年河南省衛輝市高三2月月考數學理卷 題型:解答題
(本小題滿分14分)
設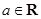 ,函數
,函數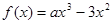
(Ⅰ)若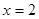 是函數
是函數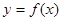 的極值點,求實數
的極值點,求實數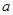 的值;
的值;
(Ⅱ)若函數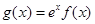 在
在 上是單調減函數,求實數
上是單調減函數,求實數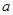 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com