
已知函數f(x)=aln x= (a為常數).
(a為常數).
(1)若曲線y=f(x)在點(1,f(1))處的切線與直線x+2y-5=0垂直,求a的值;
(2)求函數f(x)的單調區間;
(3)當x≥1時,f(x)≤2x-3恒成立,求a的取值范圍.
(1)a=1(2)f(x)的單調增區間為(0,+∞),單調減區間為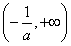 (3)a≤1.
(3)a≤1.
【解析】(1)函數f(x)的定義域為{x|x>0},f′(x)=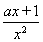 .
.
又曲線y=f(x)在點(1,f(1))處的切線與直線x+2y-5=0垂直,
所以f′(1)=a+1=2,即a=1.(4分)
(2)由f′(x)=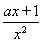 (x>0),
(x>0),
當a≥0時,
f′(x)>0恒成立,所以f(x)的單調增區間為(0,+∞).
當a<0時,
由f′(x)>0,得0<x<-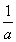 ,
,
所以f(x)的單調增區間為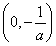 ;
;
由f′(x)<0,得x>-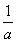 ,
,
所以f(x)的單調減區間為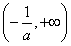 .(10分)
.(10分)
(3)設g(x)=aln x-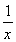 -2x+3,x∈[1,+∞),
-2x+3,x∈[1,+∞),
則g′(x)=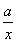 +
+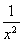 -2=
-2=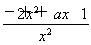 .
.
令h(x)=-2x2+ax+1,考慮到h(0)=1>0,
當a≤1時,
h(x)=-2x2+ax+1的對稱軸x=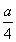 <1,
<1,
h(x)在[1,+∞)上是減函數,h(x)≤h(1)=a-1≤0,
所以g′(x)≤0,g(x)在[1,+∞)上是減函數,
所以g(x)≤g(1)=0,即f(x)≤2x2-3恒成立.
當a>1時,
令h(x)=-2x2+ax+1=0,
得x1=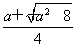 >1,x2=
>1,x2=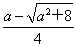 <0,
<0,
當x∈[1,x1)時,h(x)>0,即g′(x)>0,
g(x)在[1,x1)上是增函數;
當x∈(x1,+∞)時,h(x)<0,即g′(x)<0,
g(x)在(x1,+∞)上是減函數.
所以0=g(1)<g(x1),即f(x1)>2x1-3,不滿足題意.
綜上,a的取值范圍為a≤1.(16分)


科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷4練習卷(解析版) 題型:選擇題
已知正方體的棱長為1,其俯視圖是一個面積為1的正方形,側視圖是一個面積為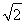 的矩形,則該正方體的正視圖的面積等于( )
的矩形,則該正方體的正視圖的面積等于( )
A.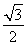 B.1 C.
B.1 C. 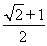 D.
D.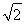
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷2練習卷(解析版) 題型:選擇題
將函數y=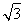 cos x+sin x(x∈R)的圖象向左平移m(m>0)個單位長度后,所得到的圖象關于y軸對稱,則m的最小值是( )
cos x+sin x(x∈R)的圖象向左平移m(m>0)個單位長度后,所得到的圖象關于y軸對稱,則m的最小值是( )
A.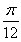 B.
B.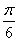 C.
C.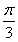 D.
D. 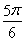
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷1練習卷(解析版) 題型:填空題
函數g(x)=x2-2 013x,若g(a)=g(b),a≠b,則g(a+b)=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)專題階段評估模擬卷1練習卷(解析版) 題型:選擇題
若a,b∈R,且ab>0,則下列不等式中,恒成立的是( )
A.a+b≥2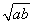 B.
B.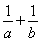 >
>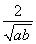
C.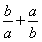 ≥2 D.a2+b2>2ab
≥2 D.a2+b2>2ab
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練解答題押題練C組練習卷(解析版) 題型:解答題
設數列{bn}滿足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求證數列{bnbn+1bn+2+n}是等差數列;
(3)設數列{Tn}滿足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-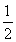 ,若存在實數p,q,對任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,試求q-p的最小值.
,若存在實數p,q,對任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,試求q-p的最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練解答題押題練B組練習卷(解析版) 題型:解答題
已知函數f(x)=-x3+x2,g(x)=aln x,a∈R.
(1)若對任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求a的取值范圍;
(2)設F(x)=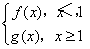 若P是曲線y=F(x)上異于原點O的任意一點,在曲線y=F(x)上總存在另一點Q,使得△POQ中的∠POQ為鈍角,且PQ的中點在y軸上,求a的取值范圍.
若P是曲線y=F(x)上異于原點O的任意一點,在曲線y=F(x)上總存在另一點Q,使得△POQ中的∠POQ為鈍角,且PQ的中點在y軸上,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練填空題押題練F組練習卷(解析版) 題型:填空題
在平面直角坐標系xOy中,直線3x+4y-5=0與圓x2+y2=4相交于A,B兩點,則弦AB的長等于________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學(文)三輪專題體系通關訓練填空題押題練C組練習卷(解析版) 題型:填空題
已知集合A={2,5},在A中可重復的依次取出三個數a,b,c,則“以a,b,c為邊恰好構成三角形”的概率是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com