中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

對定義在區間l，上的函數，若存在開區間和常數C，使得對任意的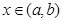都有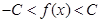，且對任意的x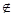（a，b）都有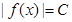恒成立，則稱函數為區間I上的“Z型”函數．

    （I）求證：函數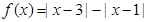是R上的“Z型”函數；

    （Ⅱ）設是（I）中的“Z型”函數，若不等式對任意的x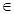R恒成立，求實數t的取值范圍．

 

【答案】

（Ⅰ）函數為上的“型”函數. （Ⅱ）或.

【解析】本試題主要是考查了絕對值不等式和絕對值函數的運用。

（1）因為根據新定義可知，函數是否是R上的“Z型”函數，只要判定。對任意的都有，且對任意的都有恒成立即可

（2）不等式對一切的恒成立，只要即可這樣可知得到t的取值范圍。

 

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

（2013•成都二模）對于定義在區間D上的函數f（x），若滿足對?x1，x2∈D，且x1＜x2時都有 f（x1）≥f（x2），則稱函數f（x）為區間D上的“非增函數”．若f（x）為區間[0，1]上的“非增函數”且f（0）=l，f（x）+f（l-x）=l，又當x∈[0，
1
4
]時，f（x）≤-2x+1恒成立．有下列命題：
①?x∈[0，1]，f（x）≥0；
②當x1，x2∈[0，1]且x1≠x2，時，f（x1）≠f（x）
③?x∈[
1
4
，
3
4
]時，都有f(x)=
1
2

④函數f（x）的圖象關于點(
1
2
，
1
2
)對稱
其中你認為正確的所有命題的序號為
①③④
①③④
．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2013•成都二模）對于定義在區間D上的函數f（x），若滿足對?x1，x2∈D，且x1＜x2時都有 f（x1）≥f（x2），則稱函數f（x）為區間D上的“非增函數”．若f（x）為區間[0，1]上的“非增函數”且f（0）=l，f（x）+f（l-x）=l，又當x∈[0，
1
4
]時，f（x）≤-2x+1恒成立．有下列命題：
①?x∈[0，1]，f（x）≥0；
②當x1，x2∈[0，1]且x1≠x2，時，f（x1）≠f（x）
③f（
1
8
）+f（
5
11
）+f（
7
13
）+f（
7
8
）=2；
④當x∈[0，
1
4
]時，f（f（x））≤f（x）．
其中你認為正確的所有命題的序號為
①③④
①③④
．

查看答案和解析>>

科目：高中數學 來源：2012高三數學一輪復習單元練習題　函數(6) 題型：044

設f(x)是定義在[0，1]上的函數，若存在x*∈(0，1)，使得f(x)在[0，x*]上單調遞增，在[x*，1]上單調遞減，則稱f(x)為[0，1]上的單峰函數，x*為峰點，包含峰點的區間為含峰區間．

對任意的[0，l]上的單峰函數f(x)，下面研究縮短其含峰區間長度的方法．

(1)證明：對任意的x1，x2∈(0，1)，x1＜x2，若f(x1)≥f(x2)，則(0，x2)為含峰區間；若f(x1)≤f(x2)，則(x*，1)為含峰區間；

(2)對給定的r(0＜r＜0.5＝，證明：存在x1，x2∈(0，1)，滿足x2－x1≥2r，使得由(Ⅰ)所確定的含峰區間的長度不大于0.5＋r；

(3)選取x1，x2∈(0，1)，x1＜x2，由(Ⅰ)可確定含峰區間為(0，x2)或(x1，1)，在所得的含峰區間內選取x3，由x3與x1或x3與x2類似地可確定一個新的含峰區間．在第一次確定的含峰區間為(0，x2)的情況下，試確定x1，x2，x3的值，滿足兩兩之差的絕對值不小于0.02，且使得新的含峰區間的長度縮短到0.34．(區間長度等于區間的右端點與左端點之差)

查看答案和解析>>

科目：高中數學 來源：安徽省安慶市示范高中09-10學年高一五校協作期中考試 題型：解答題

 設f（x）是定義在[0，1]上的函數，若存在x*∈（0，1），使得f（x）在[0， x*]上單調遞增，在[x*，1]上單調遞減，則稱f（x）為[0，1]上的單峰函數，x*為峰點，包含峰點的區間為含峰區間．對任意的[0，l]上的單峰函數f（x），下面研究縮短其含峰區間長度的方法.

   （1）證明：對任意的x1，x2∈（0，1），x1＜x2，若f（x1）≥f（x2），則（0，x2）為含峰區間；若f（x1）≤f（x2），則（x*，1）為含峰區間； 

   （2）對給定的r（0＜r＜0.5＝，證明：存在x1，x2∈（0，1），滿足x2－x1≥2r，使得由

       （I）所確定的含峰區間的長度不大于0.5＋r； 

   （3）選取x1，x2∈（0，1），x1＜x2，由（I）可確定含峰區間為（0，x2）或（x1，1），在所得的含峰區間內選取x3，由x3與x1或x3與x2類似地可確定一個新的含峰區間．在第一次確定的含峰區間為（0，x2）的情況下，試確定x1，x2，x3的值，滿足兩兩之差的絕對值不小于0.02，且使得新的含峰區間的長度縮短到0.34.（區間長度等于區間的右端點與左端點之差）

 

 

 

 

 

 

 

 

查看答案和解析>>

同步練習冊答案