
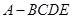 中,平面
中,平面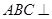 平面
平面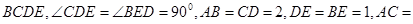
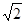 .
.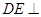 平面
平面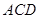 ;
;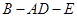 的大小
的大小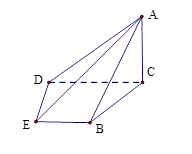
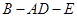 的大小是
的大小是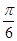 .
.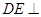 平面
平面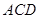 ,證明線面垂直,先證線線垂直,即證線和平面內兩條相交直線垂直,由已知可得
,證明線面垂直,先證線線垂直,即證線和平面內兩條相交直線垂直,由已知可得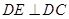 ,只需證明
,只需證明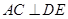 ,或
,或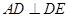 ,由已知平面
,由已知平面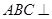 平面
平面 ,只需證明
,只需證明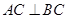 ,就得
,就得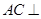 平面
平面 ,即
,即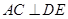 ,而由已知
,而由已知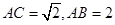 ,在直角梯形
,在直角梯形 中,易求
中,易求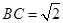 ,從而滿足
,從而滿足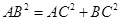 ,即得
,即得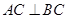 ,問題得證;(2)求二面角
,問題得證;(2)求二面角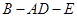 的大小,可用傳統方法,也可用向量法,用傳統方法,關鍵是找二面角的平面角,可利用三垂線定理來找,但本題不存在利用三垂線定理的條件,因此利用垂面法,即作
的大小,可用傳統方法,也可用向量法,用傳統方法,關鍵是找二面角的平面角,可利用三垂線定理來找,但本題不存在利用三垂線定理的條件,因此利用垂面法,即作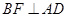 ,與
,與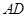 交于點
交于點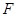 ,過點
,過點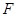 作
作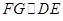 ,與
,與 交于點
交于點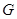 ,連結
,連結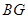 ,由(1)知,
,由(1)知,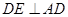 ,則
,則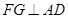 ,,所以
,,所以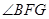 是二面角
是二面角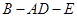 的平面角,求出
的平面角,求出 的三條邊,利用余弦定理,即可求出二面角
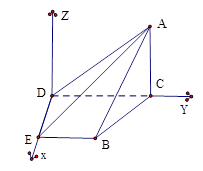
的三條邊,利用余弦定理,即可求出二面角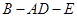 的大小,用向量法,首先建立空間坐標系,先找三條兩兩垂直的直線作為坐標軸,觀察幾何圖形可知,以
的大小,用向量法,首先建立空間坐標系,先找三條兩兩垂直的直線作為坐標軸,觀察幾何圖形可知,以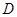 為原點,分別以射線
為原點,分別以射線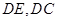 為
為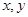 軸的正半軸,建立空間直角坐標系
軸的正半軸,建立空間直角坐標系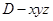 ,寫出個點坐標,設出設平面
,寫出個點坐標,設出設平面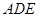 的法向量為
的法向量為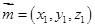 ,平面
,平面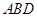 的法向量為
的法向量為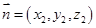 ,求出它們的一個法向量,利用法向量的夾角與二面角的關系,即可求出二面角
,求出它們的一個法向量,利用法向量的夾角與二面角的關系,即可求出二面角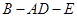 的大小.
的大小. 中,由
中,由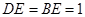 ,
,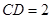 得,
得,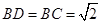 ,由
,由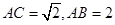 ,則
,則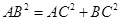 ,即
,即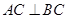 ,又平面
,又平面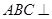 平面
平面 ,從而
,從而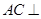 平面
平面 ,所以
,所以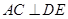 ,又
,又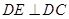 ,從而
,從而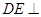 平面
平面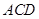 ;
;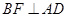 ,與
,與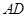 交于點
交于點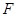 ,過點
,過點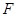 作
作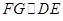 ,與
,與 交于點
交于點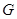 ,連結
,連結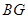 ,由(1)知,
,由(1)知,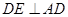 ,則
,則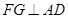 ,,所以
,,所以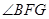 是二面角
是二面角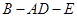 的平面角,在直角梯形
的平面角,在直角梯形 中,由
中,由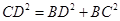 ,得
,得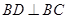 ,又平面
,又平面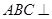 平面
平面 ,得
,得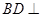 平面
平面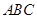 ,從而,
,從而,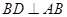 ,由于
,由于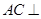 平面
平面 ,得:
,得: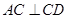 ,在
,在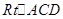 中,由
中,由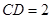 ,
,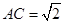 ,得
,得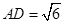 ,
,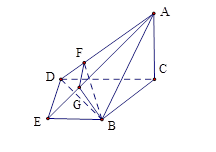
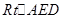 中,
中,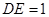 ,
,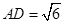 ,得
,得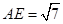 ,在
,在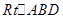 中,
中,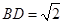 ,
,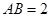 ,
,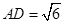 ,得
,得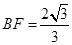 ,
,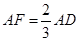 ,從而
,從而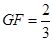 ,在
,在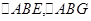 中,利用余弦定理分別可得
中,利用余弦定理分別可得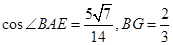 ,在
,在 中,
中,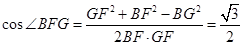 ,所以
,所以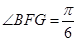 ,即二面角
,即二面角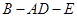 的大小是
的大小是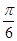 .
.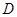 為原點,分別以射線
為原點,分別以射線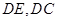 為
為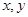 軸的正半軸,建立空間直角坐標系
軸的正半軸,建立空間直角坐標系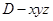 如圖所示,由題意可知各點坐標如下:
如圖所示,由題意可知各點坐標如下: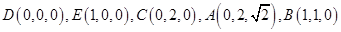 ,設平面
,設平面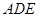 的法向量為
的法向量為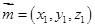 ,平面
,平面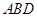 的法向量為
的法向量為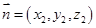 ,可算得
,可算得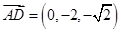 ,
,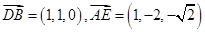 ,由
,由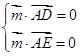 得,
得,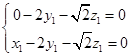 ,可取
,可取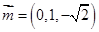 ,由
,由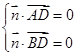 得,
得,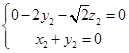 ,可取
,可取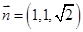 ,于是
,于是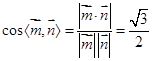 ,由題意可知,所求二面角是銳角,故二面角
,由題意可知,所求二面角是銳角,故二面角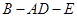 的大小是
的大小是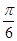 .
.


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源:不詳 題型:解答題
 是直角梯形,∠
是直角梯形,∠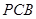 =90°,
=90°,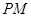 ∥
∥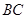 ,
,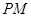 =1,
=1,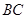 =2,又
=2,又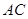 =1,∠
=1,∠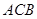 =120°,
=120°,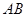 ⊥
⊥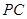 ,直線
,直線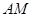 與直線
與直線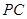 所成的角為60°.
所成的角為60°.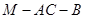 的的余弦值;
的的余弦值;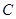 到面
到面 的距離.
的距離.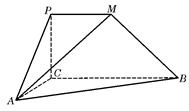
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
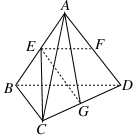
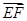 ·
·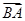 ;
;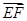 ·
·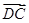 ;
;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
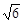 ,高CD=3,點E是線段BD上異于點B、D的動點.點F在BC邊上,且EF⊥AB.現沿EF將△BEF折起到△PEF的位置,使PE⊥AE.記
,高CD=3,點E是線段BD上異于點B、D的動點.點F在BC邊上,且EF⊥AB.現沿EF將△BEF折起到△PEF的位置,使PE⊥AE.記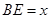 ,用
,用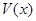 表示四棱錐P-ACFE的體積.
表示四棱錐P-ACFE的體積.
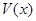 的表達式;
的表達式;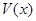 取得最大值?
取得最大值?查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
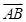 ,
,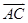 為邊的平行四邊形的面積;
為邊的平行四邊形的面積;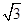 ,且a分別與
,且a分別與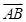 ,
,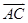 垂直,求向量a的坐標.
垂直,求向量a的坐標.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com