
定義點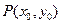 到直線
到直線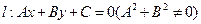 的有向距離為
的有向距離為 .已知點
.已知點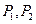 到直線
到直線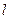 的有向距離分別是
的有向距離分別是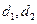 ,給出以下命題:
,給出以下命題:
①若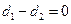 ,則直線
,則直線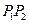 與直線
與直線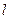 平行;②若
平行;②若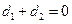 ,則直線
,則直線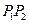 與直線
與直線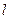 平行;
平行;
③若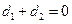 ,則直線
,則直線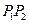 與直線
與直線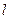 垂直;④若
垂直;④若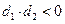 ,則直線
,則直線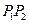 與直線
與直線 相交;其中正確命題的序號是 .
相交;其中正確命題的序號是 .
 特高級教師點撥系列答案
特高級教師點撥系列答案 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:解答題
如圖1,在直角梯形 中,
中,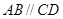 ,
,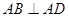 ,且
,且 .現以
.現以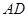 為一邊向形外作正方形
為一邊向形外作正方形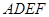 ,然后沿邊
,然后沿邊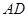 將正方形
將正方形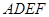 翻折,使平面
翻折,使平面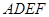 與平面
與平面 垂直,
垂直, 為
為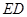 的中點,如圖2.
的中點,如圖2.
(1)求證: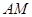 ∥平面
∥平面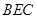 ;
;
(2)求證: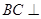 平面
平面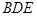 ;
;
(3)求點 到平面
到平面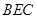 的距離.
的距離.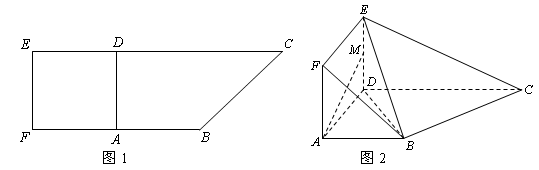
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,圓錐頂點為P,底面圓心為O,其母線與底面所成的角為22.5°,AB和CD是底面圓O上的兩條平行的弦,軸OP與平面PCD所成的角為60°.
(1)證明:平面PAB與平面PCD的交線平行于底面;
(2)求cos∠COD.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
已知兩條不同直線 、
、
 ,兩個不同平面
,兩個不同平面 、
、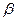 ,給出下列命題:
,給出下列命題:
①若 垂直于
垂直于 內的
內的 兩條相交直線,則
兩條相交直線,則 ⊥
⊥ ;
;
②若 ∥
∥ ,則
,則 平行于
平行于 內的所有直線;
內的所有直線;
③若

 ,
,

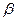 且
且 ⊥
⊥ ,則
,則
 ⊥
⊥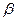 ;
;
④若

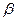 ,
, ,則
,則 ⊥
⊥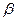 ;
;
⑤若

 ,
,

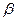 且
且 ∥
∥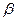 ,則
,則 ∥
∥ .
.
其中正確命題的序號是 .(把你認為正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
設 是兩條不同的直線,
是兩條不同的直線,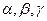 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若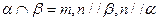 ,則
,則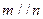 ;
;
②若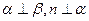 ,則
,則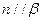 ;
;
③若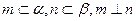 ,則
,則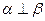 ;
;
④若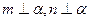 ,則
,則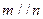 ;
;
其中正確命題有_____________.(填上你認為正確命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
設α、β、γ為彼此不重合的三個平面,ι為直線,給出下列命題:
①若α∥β,α⊥γ,則β⊥γ,
②若α⊥γ,β⊥γ,且αnβ=ι,則ι⊥γ
③若直線l與平面α內的無數條直線垂直則直線ι與平而α垂直,
④若α內存在不共線的三點到β的距離相等.則平面α平行于平面β
上面命題中,真命題的序號為 (寫出所有真命題的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com