
已知函數f(x)=cos(2x+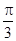 )+sin2x
)+sin2x
(1)求函數f(x)的單調遞減區間及最小正周期;
(2)設銳角△ABC的三內角A,B,C的對邊分別是a,b,c,若c=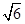 ,cosB=
,cosB=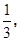
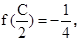 求b.
求b.
(1)最小正周期T=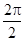 =π,f(x)的單調遞減區間是[kπ-
=π,f(x)的單調遞減區間是[kπ-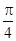 ,kπ+
,kπ+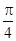 ](k∈Z).
](k∈Z).
(2) b=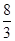 .
.
【解析】
試題分析:(1)∵f(x)=cos(2x+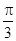 )+sin2x=cos2xcos
)+sin2x=cos2xcos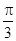 -sin2xsin
-sin2xsin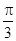 +
+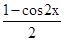
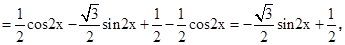
∴最小正周期T=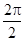 =π,令2kπ-
=π,令2kπ-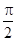 ≤2x≤2kπ+
≤2x≤2kπ+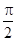 (k∈Z),得kπ-
(k∈Z),得kπ-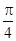 ≤x≤kπ+
≤x≤kπ+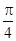 ,k∈Z,
,k∈Z,
∴f(x)的單調遞減區間是[kπ-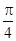 ,kπ+
,kπ+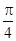 ](k∈Z).
](k∈Z).
(2)由(1)得f(x)=-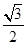 sin2x+
sin2x+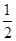 ,
,
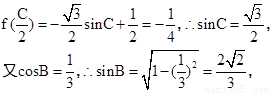
∴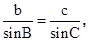 即
即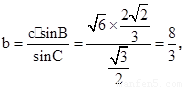 故b=
故b=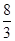 .
.
考點:本題主要考查三角函數的和差倍半公式,正弦定理的應用,三角函數的圖象和性質。
點評:中檔題,近些年,涉及三角函數、三角形的題目常常出現在高考題中,往往需要綜合應用三角公式化簡函數,以進一步研究函數的性質。應用正弦定理、余弦定理求邊長、角等,有時運用函數方程思想,問題的解決較為方便。


 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:高中數學 來源: 題型:
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| m |
| n |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com