
設函數f ( x )的定義域、值域均為R,f ( x ) 反函數為f1 ( x ),且對任意實數x,均有f ( x ) + f1 ( x )<![]() 。定義數列{an} : a0 = 8 , a1 = 10 , an = f (an1 ) , n = 1, 2 , … .
。定義數列{an} : a0 = 8 , a1 = 10 , an = f (an1 ) , n = 1, 2 , … .
(1)求證:an+1 + an1<![]() an ( n = 1 , 2 , … ) ;
an ( n = 1 , 2 , … ) ;
(2)設![]() 求證:
求證:![]() ;
;
(3)是否存在常數A和B,同時滿足;
①當n = 0 及n = 1 時,有an =![]() 成立;
成立;
②當n = 2 , 3, … 時,有an<![]() 成立。
成立。
如果存在滿足上述條件的實數A、B的值;如果不存在,證明你的結論。
解:(1)∵f ( x ) + f1 ( x )<![]() x ,令x = an , 則f ( an ) + f1 ( an )<
x ,令x = an , 則f ( an ) + f1 ( an )< ![]() an
an
an+1 + an1< ![]() an
an
(2)∵an+1< ![]() an an1
an an1
∴an+1 2an<![]() ( an 2an1 ) 即bn<
( an 2an1 ) 即bn<![]() bn1
bn1
∵b0 = a1 2a0 = 6
∴ bn<![]()
(3)由(2)可知:bn<![]()
假設存在常數A和B,使得an![]() 對n = 0, 1 成立。則
對n = 0, 1 成立。則
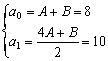 解得A = B = 4
解得A = B = 4
下面用數學歸納法證明an<![]() 對一切n≥2,n∈N*成立.
對一切n≥2,n∈N*成立.
1)當n = 2時,由an+1 + an1<![]() an , 得a2<
an , 得a2<![]() a1 a0 =
a1 a0 =![]()
∴n = 2時,an<![]() 成立。
成立。
2)假設 n = k ( k≥2 )時,不等式成立,即ak<![]() ,則
,則
ak+1<2ak + ( 6 ) ![]() <2×
<2×![]() +( 6 )
+( 6 ) ![]() =
=![]() ,
,
這說明n = k+1 時,不等式成立。
綜合1),2),可知an<![]() 對一切n≥2,n∈N成立。
對一切n≥2,n∈N成立。
∴A = B = 4 滿足題設


科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com