(本題滿分14分) 設首項為
a1,公差為
d的等差數(shù)列{
an}的前
n項和為
Sn.
已知
a7=-2,
S5=30.
(Ⅰ) 求
a1及
d;
(Ⅱ) 若數(shù)列{
bn}滿足
an=
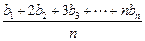
(
n∈N*),
求數(shù)列{
bn}的通項公式

.
(Ⅰ)
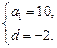
(Ⅱ)
bn=
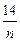
-4 (
n∈N*).
(Ⅰ) 解:由題意可知
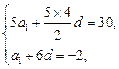
得
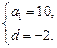
………………………………………6分
(Ⅱ) 解:由(Ⅰ)得
an=10+(
n-1)(-2)=12-2
n,
所以
b1+2
b2+3
b3+…+
nbn=
nan=
n(12-2
n),
當
n=1時,
b1=10,
當
n≥2時,
b1+2
b2+3
b3+…+(
n-1)
bn-1=(
n-1)[12-2(
n-1)],
所以
nbn=
n(12-2
n)-(
n-1)[12-2(
n-1)]=14-4
n,
故
bn=
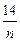
-4.
當
n=1時也成立.
所以
bn=
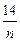
-4 (
n∈N*). ……………………………14分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
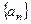
中,對一切自然數(shù)
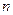
,都有
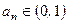
且
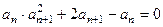
.
求證:(1)
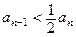
;
(2)若
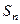
表示數(shù)列
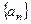
的前
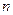
項之和,則
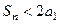
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知

是等差數(shù)列,且

(1)求

的通項公式;
(2)設

為

的前n項和,n為什么值時

最大,最大值是多少?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題10分)
已知等差數(shù)列
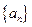
滿足
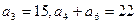
,
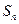
為
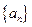
的前
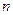
項和.
(1)求通項
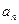
及當
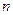
為何值時,
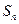
有最大值,并求其最大值。
(2)設
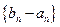
是首項為1,公比為3的等比數(shù)列,求數(shù)列
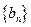
的通項公式及其前
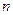
項和
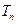
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知等差數(shù)列
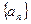
滿足:
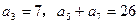
,
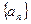
的前n項和為
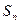
,
(1) 求
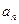
及
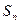
;
(2) 令
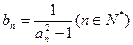
,求數(shù)列
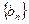
的前n項和
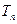
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
三個數(shù)成等差數(shù)列,其比為3:4:5,又最小數(shù)加上1后,三個數(shù)成等比數(shù)列,那么原三個數(shù)是___。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
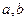
為正實數(shù),
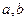
的等差中項為A;
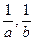
的等差中項為
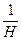
;
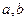
的等比中項為
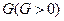
,則( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知等差數(shù)列
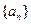
的公差為
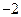
,且
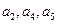
成等比數(shù)列,則
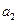
等于( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(12分)已知等差數(shù)列
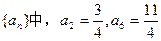
(1)求
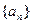
的通項公式;
(2)數(shù)列
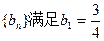
,且
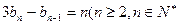
),求證
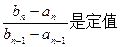
;
(3)求
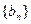
通項公式及前n項和
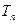
。
查看答案和解析>>

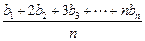 (n∈N*),
(n∈N*), .
. 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案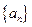 滿足
滿足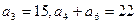 ,
,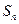 為
為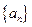 的前
的前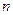 項和.
項和.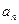 及當
及當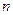 為何值時,
為何值時,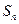 有最大值,并求其最大值。
有最大值,并求其最大值。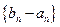 是首項為1,公比為3的等比數(shù)列,求數(shù)列
是首項為1,公比為3的等比數(shù)列,求數(shù)列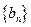 的通項公式及其前
的通項公式及其前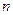 項和
項和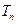 .
.