
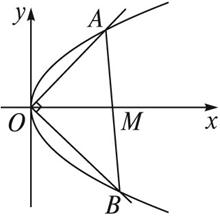
(1)證明直線AB過定點;
(2)求△AOB面積的最小值.
解:(1)設直線AB的方程為y=k(x-a),A(x1,y1),B(x2,y2).聯立方程
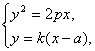 消去x得ky2-2py-2pak=0,
消去x得ky2-2py-2pak=0,
則y1y2=-2pa.又OA⊥OB.
∴y1y2=-x1x2.
由方程組消去y,得k2x2-(2k2a+2p)x+k2a2=0,則x1·x2=a2.因此,a2=2pa.∴a=2p.
故直線AB過定點(2p,0).
(2)由(1)知:AB恒過定點M(2p,0).
∴S△AOB=S△AOM+S△BOM=![]() |OM|(|y1|+|y2|)≥p(2
|OM|(|y1|+|y2|)≥p(2![]() |).
|).
又y12=2px1,y22=2px2,
∴(y1y2)2=4p2x1x2.
又∵y1y2=-x1x2,
于是|y1y2|=4p2.
故S△AOB的最小值為4p2.
綠色通道:
對于直線、曲線方程聯立求解,靈活運用整體思想及韋達定理可簡化解答;另外應注意圖形的有效利用.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
 設b>0,橢圓方程為
設b>0,橢圓方程為| x2 |
| 2b2 |
| y2 |
| b2 |
| 1 |
| 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 設b>0,橢圓方程為
設b>0,橢圓方程為| x2 |
| 2b2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| S△ | S弓 |
查看答案和解析>>
科目:高中數學 來源:廣東省高考真題 題型:解答題
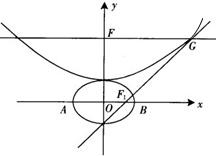
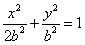 ,拋物線方程為x2=8(y-b),如圖所示,過點F(0,b+2)作x軸的平行線,與拋物線在第一象限的交點為G,已知拋物線在點G的切線經過橢圓的右焦點F1,
,拋物線方程為x2=8(y-b),如圖所示,過點F(0,b+2)作x軸的平行線,與拋物線在第一象限的交點為G,已知拋物線在點G的切線經過橢圓的右焦點F1,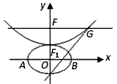
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京四中高二(上)期末數學試卷(理科)(解析版) 題型:解答題
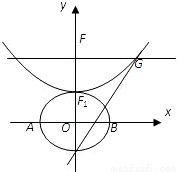 設b>0,橢圓方程為
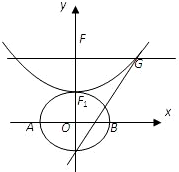
設b>0,橢圓方程為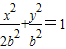 ,拋物線方程為x2=8(y-b).如圖所示,過點F(0,b+2)作x軸的平行線,與拋物線在第一象限的交點為G,已知拋物線在點G的切線經過橢圓的右焦點F1.
,拋物線方程為x2=8(y-b).如圖所示,過點F(0,b+2)作x軸的平行線,與拋物線在第一象限的交點為G,已知拋物線在點G的切線經過橢圓的右焦點F1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com