中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

（1）若函數f(x)=ax2-x-1有且僅有一個零點，求實數a的值；

（2）若函數f(x)=|4x-x2|+a有4個零點，求實數a的取值范圍.

（1）a=0或a=-（2）a的取值范圍是（-4,0）


解析:

（1）若a=0，則f(x)=-x-1,

令f(x)=0,即-x-1=0,得x=-1,故符合題意；                               2分

若a≠0，則f(x)=ax2-x-1是二次函數，

故有且僅有一個零點等價于Δ=1+4a=0，解得a=-，                      4分

綜上所述a=0或a=-.                                         6分

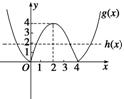
（2）若f(x)=|4x-x2|+a有4個零點，

即|4x-x2|+a=0有四個根，即|4x-x2|=-a有四個根.                    8分 

令g(x)=|4x-x2|,h(x)=-a.

作出g(x)的圖象，由圖象可知如果要使|4x-x2|=-a有四個根，                       

那么g(x)與h（x)的圖象應有4個交點.                                 12分

故需滿足0＜-a＜4,即-4＜a＜0.

∴a的取值范圍是（-4,0）.                                         14分

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

記函數f（x）的定義域為D，若存在x0∈D，使f（x0）=x0成立，則稱以（x0，x0）為坐標的點為函數f（x）圖象上的不動點．
（1）若函數f(x)=
3x+a
x+b
圖象上有兩個關于原點對稱的不動點，求實數a，b應滿足的條件；
（2）設點P（x，y）到直線y=x的距離d=
|x-y|
2
．在（1）的條件下，若a=8，記函數f（x）圖象上的兩個不動點分別為A1，A2，P為函數f（x）圖象上的另一點，其縱坐標yP＞3，求點P到直線A1A2距離的最小值及取得最小值時點P的坐標．
（3）下述命題“若定義在R上的奇函數f（x）圖象上存在有限個不動點，則不動點有奇數個”是否正確？若正確，請給予證明；若不正確，請舉一反例．若地方不夠，可答在試卷的反面．

查看答案和解析>>

科目：高中數學 來源： 題型：

記min{p，q}=
p，p≤q
q．p＞q
．
（1）若函數f(x)=min{
x
，
2
3
(x-1)}，求f（x）表達式
（2）求f(x)=min{3|x-p1|，2×3|x-p2|)}=3|x-p1|，對所有實數x成立的充分必要條件（用p1，p2表示）；
（3）若f(x)=min{3|x-p1|，2×3|x-p2|)}，且f（a）=f（b）（a，bp1，p2為實數，且a＜bp1，p2∈（a，b））求f（x）在區間[a，b]上的單調增區間的長度和（閉區間[m，n]的長度定義為n-m）．

查看答案和解析>>

科目：高中數學 來源： 題型：

對定義域分別為Df、Dg的函數y=f（x）、y=g（x），規定：函數h(x)=
f(x)•g(x)(x∈Df且x∈Dg)
f(x)(x∈Df且x∉Dg)
g(x)(x∉Df且x∈Dg).

（1）若函數f(x)=
1
x-1
，g（x）=x2，寫出函數h（x）的解析式；
（2）求（1）問中函數h（x）的值域．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知a，b為正實數．
（1）若函數f(x)=
lnxx
，求f（x）的單調區間
（2）若e＜a＜b（e為自然對數的底），求證：ab＞ba；（3）求滿足ab=ba（a≠b）的所有正整數a，b的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2010•湖北模擬）已知a＞0，a≠1，若函數f(x)=
4
4-x2
-
1
2+x
(x＞-2)
loga(-x)(x≤-2)
在點x=-2處連續，則a=
16
16
．

查看答案和解析>>

同步練習冊答案