
已知函數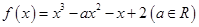 .
.
(1)當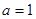 時,求函數
時,求函數 的極值;
的極值;
(2)若對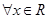 ,有
,有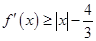 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
(1)極大值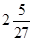 ,極小值
,極小值 ;(2)
;(2)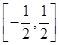 .
.
解析試題分析:(1)將
科目:高中數學
來源:
題型:解答題
已知函數f(x)=xlnx-
科目:高中數學
來源:
題型:解答題
已知函數f(x)=ln x,g(x)=
科目:高中數學
來源:
題型:解答題
(12分)(2011•陜西)如圖,從點P1(0,0)做x軸的垂線交曲線y=ex于點Q1(0,1),曲線在Q1點處的切線與x軸交于點P2,再從P2做x軸的垂線交曲線于點Q2,依次重復上述過程得到一系列點:P1,Q1;P2,Q2…;Pn,Qn,記Pk點的坐標為(xk,0)(k=1,2,…,n).
科目:高中數學
來源:
題型:解答題
設函數f(x)=ln x-ax,g(x)=ex-ax,其中a為實數.若f(x)在(1,+∞)上是單調減函數,且g(x)在(1,+∞)上有最小值,求a的取值范圍.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區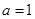 代入函數
代入函數 的解析式,利用導數結合表格求出函數
的解析式,利用導數結合表格求出函數 的極大值與極小值;(2)對
的極大值與極小值;(2)對 的符號進行分三類討論①
的符號進行分三類討論①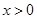 ;②
;②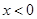 ;③
;③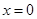 ,主要是取絕對值符號,結合基本不等式求出參數
,主要是取絕對值符號,結合基本不等式求出參數 的取值范圍,最后再相應地取
的取值范圍,最后再相應地取 在三種情況下對應取值范圍的交集.
在三種情況下對應取值范圍的交集.
(1)當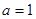 時,
時,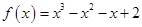 ,
,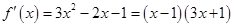 ,
,
令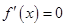 ,解得
,解得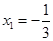 ,
,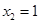 ,
,
當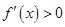 時,得
時,得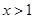 或
或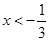 ;
;
當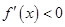 時,得
時,得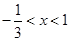 ,
,
當 變化時,
變化時,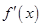 ,
, 的變化情況如下表:
的變化情況如下表:
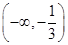
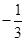
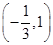

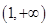
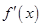
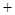

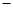

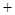

單調遞增 

同步練習浙江教育出版社系列答案
同步訓練與單元測試系列答案
同步訓練與期中期末闖關系列答案
同步訓練與中考闖關系列答案
階梯訓練系列答案
王朝霞小升初重點校系列答案
專項卷和真題卷系列答案
文曲星中考總復習系列答案
問題引領系列答案
先鋒題典系列答案
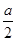 x2.
x2.
(1)當a=1時,函數y=f(x)有幾個極值點?
(2)是否存在實數a,使函數f(x)=xlnx-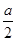 x2有兩個極值?若存在,求實數a的取值范圍;若不存在,請說明理由.
x2有兩個極值?若存在,求實數a的取值范圍;若不存在,請說明理由. x2-bx(b為常數).
x2-bx(b為常數).
(1)函數f(x)的圖像在點(1,f(1))處的切線與g(x)的圖像相切,求實數b的值;
(2)設h(x)=f(x)+g(x),若函數h(x)在定義域上存在單調減區間,求實數b的取值范圍;
(3)若b>1,對于區間[1,2]上的任意兩個不相等的實數x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求實數b的取值范圍.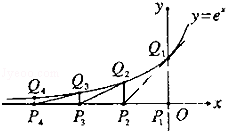
(Ⅰ)試求xk與xk﹣1的關系(2≤k≤n);
(Ⅱ)求|P1Q1|+|P2Q2|+|P3Q3|+…+|PnQn|.
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號