
如圖所示,在直三棱柱 中,
中,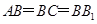 ,
, 為
為 的中點.
的中點.
(Ⅰ) 若AC1⊥平面A1BD,求證:B1C1⊥平面ABB1A1;
(Ⅱ)在(Ⅰ)的條件下,設AB=1,求三棱錐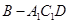 的體積.
的體積.
(I)通過證明“線線垂直”,得到“線面垂直”, ⊥面
⊥面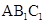 ,得到
,得到 .
.
又在直棱柱 中,
中, ,得到
,得到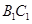 ⊥平面
⊥平面 .
.
(II)三棱錐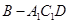 的體積
的體積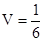 .
.
解析試題分析:(I)(I)通過證明“線線垂直”,得到“線面垂直”, ⊥面
⊥面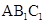 ,得到
,得到 .
.
又在直棱柱 中,
中, ,得到
,得到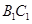 ⊥平面
⊥平面 .
.
(II)為確定三棱錐的體積,應注意明確“底面”“高”,注意遵循“一作,二證,三計算”的解題步驟.通過證明“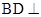 平面
平面 ”.明確
”.明確 就是三棱錐
就是三棱錐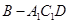 的高.
的高.
解答此類問題,容易出現的錯誤是忽視證明,利用直觀感覺確定高.
試題解析:(I)直三棱柱 中,∵
中,∵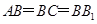 ,∴四邊形
,∴四邊形 為正方形,
為正方形,
∴ ,
,
又∵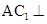 面
面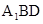 ,∴
,∴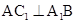 ,∴
,∴ ⊥面
⊥面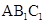 ,∴
,∴ .
.
又在直棱柱 中,
中, ,∴B1C1⊥平面ABB1A1.
,∴B1C1⊥平面ABB1A1.
(II)∵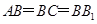 ,
, 為
為 的中點,∴
的中點,∴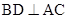 .
.
∴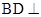 平面
平面 .
.
∴ 就是三棱錐
就是三棱錐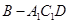 的高.
的高.
由(I)知B1C1⊥平面ABB1A1,∴ 平面ABB1A1.
平面ABB1A1.
∴ .∴
.∴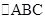 是直角等腰三角形.
是直角等腰三角形.
又∵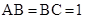 ,∴
,∴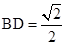 ,
,
∴ ,
,
∴三棱錐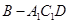 的體積
的體積 .
.
考點:垂直關系、體積計算.


科目:高中數學 來源: 題型:解答題
如圖,已知四棱錐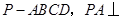 平面
平面 ,底面
,底面 為直角梯形,
為直角梯形,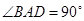 ,且
,且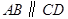 ,
,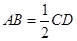 .
.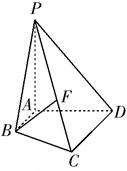
(1)點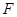 在線段
在線段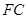 上運動,且設
上運動,且設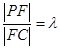 ,問當
,問當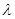 為何值時,
為何值時,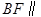 平面
平面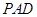 ,并證明你的結論;
,并證明你的結論;
(2)當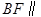 面
面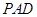 ,且
,且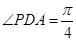 ,
,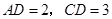 求四棱錐
求四棱錐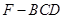 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,△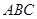 中,
中,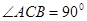 ,
,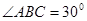 ,
,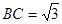 ,在三角形內挖去一個半圓(圓心
,在三角形內挖去一個半圓(圓心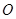 在邊
在邊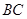 上,半圓與
上,半圓與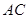 、
、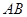 分別相切于點
分別相切于點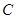 、
、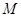 ,與
,與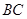 交于點
交于點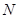 ),將△
),將△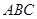 繞直線
繞直線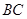 旋轉一周得到一個旋轉體。
旋轉一周得到一個旋轉體。
(1)求該幾何體中間一個空心球的表面積的大小;
(2)求圖中陰影部分繞直線 旋轉一周所得旋轉體的體積.
旋轉一周所得旋轉體的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,三棱柱ABC—A1B1C1的側棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上中點,F是AB中點,AC = 1,BC = 2,AA1 = 4.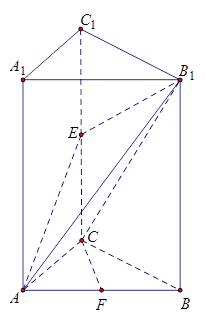
(1)求證:CF∥平面AEB1;(2)求三棱錐C-AB1E的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四棱柱ABCD-A1B1C1D1中,已知平面AA1C1C丄平面ABCD,且AB=BC=CA=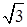 ,AD=CD=1.
,AD=CD=1.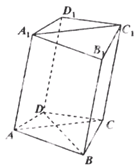
 求證:BD⊥AA1;
求證:BD⊥AA1; 若四邊形
若四邊形 是菱形,且
是菱形,且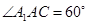 ,求四棱柱
,求四棱柱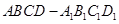 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在四棱錐P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E為PD的中點,PA=2AB=2.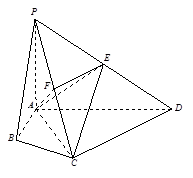
(Ⅰ)若F為PC的中點,求證PC⊥平面AEF;
(Ⅱ)求四棱錐P-ABCD的體積V.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知某幾何體的俯視圖是如圖所示的矩形,正視圖(或稱主視圖)是一個底邊長為8、高為4的等腰三角形,側視圖(或稱左視圖)是一個底邊長為6、高為4的等腰三角形.
(1)求該幾何體的體積V;
(2)求該幾何體的側面積S.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com