Question

（2003•北京）有三個(gè)新興城鎮(zhèn)，分別位于A，B，C三點(diǎn)處，且AB=AC=13km，BC=10km．今計(jì)劃合建一個(gè)中心醫(yī)院，為同時(shí)方便三鎮(zhèn)，準(zhǔn)備建在BC的垂直平分線(xiàn)上的P點(diǎn)處，（建立坐標(biāo)系如圖）
（Ⅰ）若希望點(diǎn)P到三鎮(zhèn)距離的平方和為最小，點(diǎn)P應(yīng)位于何處？
（Ⅱ）若希望點(diǎn)P到三鎮(zhèn)的最遠(yuǎn)距離為最小，點(diǎn)P應(yīng)位于何處？

Answer 1

分析：（I）設(shè)P的坐標(biāo)為（0，y），表示出P至三鎮(zhèn)距離的平方和，利用配方法，即可得到建立；
（II）P至三鎮(zhèn)的最遠(yuǎn)距離為g(x)=

25+y2 ，當(dāng) 25+y2 ≥|12-y| |12-y|，當(dāng) 25+y2 ＜|12-y|.

解法一：確定函數(shù)的單調(diào)性，即可求最值，從而可得點(diǎn)P的坐標(biāo)；
解法二：作出函數(shù)的圖象，結(jié)合圖象，可得結(jié)論；
解法三：結(jié)合圖形，分類(lèi)討論，確定點(diǎn)P與外心M重合時(shí)，P到三鎮(zhèn)的最遠(yuǎn)距離最小．

解答：解：（Ⅰ）設(shè)P的坐標(biāo)為（0，y），則P至三鎮(zhèn)距離的平方和為f（y）=2（25+y²）+（12-y）²=3（y-4）²+146．
所以，當(dāng)y=4時(shí)，函數(shù)f（y）取得最小值．
答：點(diǎn)P的坐標(biāo)是（0，4）．
（Ⅱ）解法一：P至三鎮(zhèn)的最遠(yuǎn)距離為g(x)=

25+y2 ，當(dāng) 25+y2 ≥|12-y| |12-y|，當(dāng) 25+y2 ＜|12-y|.

由

25+y2

≥|12-y|解得y≥

119

24

，記y*=

119

24

，于是g(x)=

25+y2 ，當(dāng)y≥y* |12-y|，當(dāng)y＜y*.

因?yàn)?span id="i2awyamu" class="MathJye">

25+y2

在[y^*，+∞）上是增函數(shù)，而|12-y|在（-∞，y^*]上是減函數(shù)．
所以y=y^*時(shí)，函數(shù)g（y）取得最小值．
答：點(diǎn)P的坐標(biāo)是(0，

119

24

)；
解法二：P至三鎮(zhèn)的最遠(yuǎn)距離為 g(x)=

25+y2 ，當(dāng) 25+y2 ≥|12-y| |12-y|，當(dāng) 25+y2 ＜|12-y|.

由

25+y2

≥|12-y|解得y≥

119

24

，記y*=

119

24

，于是g(x)=

25+y2 ，當(dāng)y≥y* |12-y|，當(dāng)y＜y*.

函數(shù)x=g（y）的圖象如圖（a），
因此，當(dāng)y=y^*時(shí)，函數(shù)g（y）取得最小值．
答：點(diǎn)P的坐標(biāo)是(0，

119

24

)；
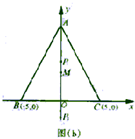
解法三：因?yàn)樵凇鰽BC中，AB=AC=13，且，

AC2-OC2

=12＞5=OC，∠ACB=

π

4

，如圖(b)．
所以△ABC的外心M在線(xiàn)段AO上，其坐標(biāo)為(0，

119

24

)，且AM=BM=CM．
當(dāng)P在射線(xiàn)MA上，記P為P₁；
當(dāng)P在射線(xiàn)MA的反向延長(zhǎng)線(xiàn)上，記P為P₂，這時(shí)P到A、B、C三點(diǎn)的最遠(yuǎn)距離為P₁C和P₂A，且P₁C≥MC，P₂A≥MA，所以點(diǎn)P與外心M重合時(shí)，P到三鎮(zhèn)的最遠(yuǎn)距離最小．
答：點(diǎn)P的坐標(biāo)是(0，

119

24

)；

點(diǎn)評(píng)：本小題主要考查函數(shù)，不等式等基本知識(shí)，考查運(yùn)用數(shù)學(xué)知識(shí)分析問(wèn)題和解決問(wèn)題的能力．