
(Ⅰ)求f(0)和f(1)的值;
(Ⅱ)設Pn-1Pn的斜率為kn(n=1,2,3,4,5),判斷k1,k2,k3,k4,k5的大小關系;
(Ⅲ)證明:當x∈(0,1)時,f(x)<x;
(Ⅳ)求由函數y=x與y=f(x)的圖象所圍成圖形的面積(用a1,a2,a3,a4,a5表示).
20.本小題主要考查函數、不等式等基本知識,考查邏輯思維能力、分析問題和解決問題的能力.
(Ⅰ)解:f(0)=![]() =0,
=0,
f(1)=![]() =1.
=1.
(Ⅱ)解:kn=![]() =
=![]() ,n=1,2,…,5,
,n=1,2,…,5,
因為a1<a2<a3<a4<a5,
所以k1<k2<k3<k4<k5.
(Ⅲ)證明:由于f(x)的圖象是連接各點Pn(xn,yn)(n=0,1,…,5)的折線,要證明f(x)<x(0<x<1),只需證明f(xn)<xn(n=1,2,3,4).事實上,當x∈(xn-1,xn)時,
f(x)=![]() (x-xn-1)+f(xn-1)
(x-xn-1)+f(xn-1)
=![]() f(xn-1)+
f(xn-1)+![]() f(xn)
f(xn)
<![]() xn-1+
xn-1+![]() xn=x.
xn=x.
下面證明f(xn)<xn .
證法一:
對任何n(n=1,2,3,4),
5(a1+…+an)=[n+(5-n)](a1+…+an)
=n(a1+…+an)+(5-n)(a1+…+an)
≤n(a1+…+an)+(5-n)nan
=n[a1+…+an+(5-n)an]
<n(a1+…+an+an+1+…+a5)=nT,
所以f(xn)=![]() <
<![]() =xn .
=xn .
證法二:
對任何n(n=1,2,3,4),
當kn<1時,
yn=(y1-y0)+(y2-y1)+…+(yn-yn-1)
=![]() (k1+k2+…+kn)<
(k1+k2+…+kn)<![]() =xn.
=xn.
當kn≥1時,
yn=y5-(y5-yn)
=1-[(yn+1-yn)+(yn+2-yn+1)+…+(y5-y4)]
=1-![]() (kn+1+kn+2+…+k5)<1-
(kn+1+kn+2+…+k5)<1-![]() (5-n)=
(5-n)=![]() =xn,
=xn,
綜上,f(xn)<xn.
(Ⅳ)解:設S1為[0,1]上折線f(x)與x軸及直線x=1所圍成圖形的面積,則
S1=![]() (y0+y1)(x1-x0)+
(y0+y1)(x1-x0)+![]() (y1+y2)(x2-x1)+
(y1+y2)(x2-x1)+![]() (y2+y3)(x3-x2)+
(y2+y3)(x3-x2)+![]() (y3+y4)(x4-x3)+
(y3+y4)(x4-x3)+![]() (y4+y5)(x5-x4)
(y4+y5)(x5-x4)
=![]() (2y1+2y2+2y3+2y4+y5)
(2y1+2y2+2y3+2y4+y5)
=![]() [a1+(a1+a2)+(a1+a2+a3)+(a1+a2+a3+a4)]+
[a1+(a1+a2)+(a1+a2+a3)+(a1+a2+a3+a4)]+![]()
=![]() (
(
直線y=x與折線y=f(x)所圍成圖形的面積為
S=![]() -S1=
-S1=![]() .
.


科目:高中數學 來源: 題型:
| n |
| 5 |
| 1 |
| T |
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)求f(0)和f(1)的值;
(2)設Pn-1Pn的斜率為kn(n=1,2,3,4,5),判斷k1、k2、k3、k4、k5的大小關系;
(3)證明當x∈(0,1)時,f(x)<x.
查看答案和解析>>
科目:高中數學 來源: 題型:
(Ⅰ)求f(0)和f(1)的值;
(Ⅱ)設Pn-1Pn的斜率為kn(n=1,2,3,4,5),判斷k1,k2,k3,k4,k5的大小關系;
(Ⅲ)證明:f(xn)<xn(n=1,2,3,4).
查看答案和解析>>
科目:高中數學 來源:2013年北京市通州區高考數學一模試卷(理科)(解析版) 題型:解答題
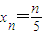 ,
,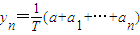 (n=0,1,2,3,4,5),作函數y=f(x),使其圖象為逐點依次連接點Pn(xn,yn)(n=0,1,2,3,4,5)的折線.
(n=0,1,2,3,4,5),作函數y=f(x),使其圖象為逐點依次連接點Pn(xn,yn)(n=0,1,2,3,4,5)的折線.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com