
某停車場臨時停車按時段收費,收費標準為:每輛汽車一次停車不超過1小時收費6元,超過1小時的部分每小時收費8元(不足1小時按1小時計算).現有甲、乙兩人在該場地停車,兩人停車都不超過4小時.
(Ⅰ)若甲停車1小時以上且不超過2小時的概率為 ,停車付費多于14元的概率為
,停車付費多于14元的概率為 ,求甲停車付費6元的概率;
,求甲停車付費6元的概率;
(Ⅱ)若甲、乙兩人每人停車的時長在每個時段的可能性相同,求甲乙二人停車付費之和為28元的概率.
(1)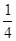 ;(2)
;(2) 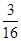 .
.
解析試題分析:(1根據題意,可知,根據停車的時間可以把事件分為4個,分別是“一次停車不超過1小時”的時間為A,“一次停車不超過2小時”的時間為B,“一次停車2到3小時”的時間為C,“一次停車3到4小時”的時間為D,可以判斷出P(B)= , P(C+D)=
, P(C+D)= , 又事件A,C,D互斥,所以可得出事件A的概率P(A)=
, 又事件A,C,D互斥,所以可得出事件A的概率P(A)= .
.
(2)列出甲,乙停車時間的所有基本事件,共計16個,可以得出“甲乙二人停車付費之和為28元”的事件有3個,所以可得出“甲乙二人停車付費之和為28元”的事件的概率.
試題解析:(Ⅰ)設“一次停車不超過1小時”的時間為A,“一次停車不超過2小時”的時間為B,“一次停車2到3小時”的時間為C,“一次停車3到4小時”的時間為D, 3分
由已知P(B)= , P(C+D)=
, P(C+D)= ,又事件A,C,D互斥,所以P(A)=
,又事件A,C,D互斥,所以P(A)= .
.
所以甲停車付費6元的概率是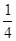 . 6分
. 6分
(Ⅱ)甲,乙停車時間的基本事件有16個:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4), 9分
“甲乙二人停車付費之和為28元”的事件有3個:(1,3),(2,2),(3,1)所以概率是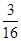 .
.
考點:古典概型.


科目:高中數學 來源: 題型:解答題
袋中裝有編號為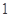 的球
的球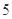 個,編號為
個,編號為 的球
的球 個,這些球的大小完全一樣。
個,這些球的大小完全一樣。
(1)從中任意取出四個,求剩下的四個球都是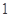 號球的概率;
號球的概率;
(2)從中任意取出三個,記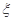 為這三個球的編號之和,求隨機變量
為這三個球的編號之和,求隨機變量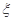 的分布列及其數學期望
的分布列及其數學期望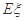 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某企業主要生產甲、乙兩種品牌的空調,由于受到空調在保修期內維修費等因素的影響,企業生產每臺空調的利潤與該空調首次出現故障的時間有關,甲、乙兩種品牌空調的保修期均為3年,現從該廠已售出的兩種品牌空調中各隨機抽取50臺,統計數據如下:
| 品牌 | 甲 | 乙 | |||||
| 首次出現故障時間 x年 |  |  |  |  |  |  |  |
| 空調數量(臺) | 1 | 2 | 4 | 43 | 2 | 3 | 45 |
| 每臺利潤(千元) | 1 | 2 | 2.5 | 2.7 | 1.5 | 2.6 | 2.8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某商場為吸引顧客消費推出一項優惠活動.活動規則如下:消費額每滿100元可轉動如圖所示的轉盤一次,并獲得相應金額的返券,假定指針等可能地停在任一位置.若指針停在A區域返券60元;停在B區域返券30元;停在C區域不返券.例如:消費218元,可轉動轉盤2次,所獲得的返券金額是兩次金額之和.
(1)若某位顧客消費128元,求返券金額不低于30元的概率;
(2)若某位顧客恰好消費280元,并按規則參與了活動,他獲得返券的金額記為 (元).求隨機變量
(元).求隨機變量 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某大學開設甲、乙、丙三門選修課,學生是否選修哪門課互不影響.已知某學生只選修甲的概率為0.08,只選修甲和乙的概率是0.12,至少選修一門的概率是0.88,用ξ表示該學生選修的課程門數和沒有選修的課程門數的乘積.
(1)記“函數f(x)=x2+ξx為R上的偶函數”為事件A,求事件A的概率;
(2)求ξ的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
從12個同類產品(其中10個是正品,2個是次品)中任意抽取3個,(1)3個都是
正品;(2)至少有1個是次品;(3)3個都是次品;(4)至少有1個是正品,上列四個事件中為
必然事件的是________ (寫出所有滿足要求的事件的編號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com