
已知點 ,
, 的坐標分別是
的坐標分別是 ,
, .直線
.直線 ,
, 相交于點
相交于點 ,且它們的斜率之積為
,且它們的斜率之積為 .
.
(1)求點 的軌跡
的軌跡 的方程;
的方程;
(2)若過點 的兩直線
的兩直線 和
和 與軌跡
與軌跡 都只有一個交點,且
都只有一個交點,且 ,求
,求 的值;
的值;
(3)在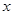 軸上是否存在兩個定點
軸上是否存在兩個定點 ,
, ,使得點
,使得點 到點
到點 的距離與到點
的距離與到點 的距離的比恒為
的距離的比恒為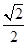 ,若存在,求出定點
,若存在,求出定點 ,
, ;若不存在,請說明理由.
;若不存在,請說明理由.
(1)軌跡 的方程為
的方程為

(2)
(3)存在定點 ,
, 或
或 ,
,
【解析】
試題分析:解: (1)設點 的坐標為
的坐標為
由題可知 ,即
,即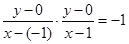 ,
,
化簡得  ,
,
所以點 的軌跡
的軌跡 的方程為
的方程為
 4分
4分
(2)分四種情況討論
情況一:當直線 和
和 都與
都與 相切時,直線
相切時,直線 和
和 與軌跡
與軌跡 都只有一個交點。
都只有一個交點。
設直線 的方程為
的方程為 ,即
,即
由 可知直線
可知直線 的方程為
的方程為 ,即
,即
因為直線 和
和 都與
都與 相切,所以
相切,所以 解得
解得 。
6分
。
6分
情況二:當直線 過點
過點 ,直線
,直線 過點
過點 時,直線
時,直線 和
和 與軌跡
與軌跡 都只有一個交點。
都只有一個交點。
此時直線 的斜率
的斜率 ,直線
,直線 的斜率
的斜率
由 知
知 ,解得
,解得 。
7分
。
7分
情況三:當直線 過點
過點 ,直線
,直線 與
與 相切時,直線
相切時,直線 和
和 與軌跡
與軌跡 都只有一個交點。
都只有一個交點。
直線 的斜率
的斜率 ,由
,由 知直線
知直線 的斜率
的斜率
故直線 的方程為
的方程為 ,即
,即
因為直線 與
與 相切,所以
相切,所以 解得
解得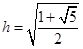 。
。
情況四:當直線 過點
過點 ,直線
,直線 與
與 相切時,直線
相切時,直線 和
和 與軌跡
與軌跡 都只有一個交點。
都只有一個交點。
直線 的斜率
的斜率 ,由
,由 知直線
知直線 的斜率
的斜率
故直線 的方程為
的方程為 ,即
,即
因為直線 與
與 相切,所以
相切,所以 解得
解得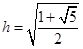 。
10分
。
10分
綜上所述: 的值為
的值為 ,1,
,1, 。
。
(3)假設存在定點 ,
, ,設
,設 ,
, ,
,
則 化簡整理得
化簡整理得 (*) 11分
(*) 11分
由于 滿足
滿足 ,故(*)式可化為
,故(*)式可化為 12分
12分
故 解得
解得 或
或
故存在定點 ,
, 或
或 ,
, ,使得點
,使得點 到點
到點 的距離與到點
的距離與到點 的距離的比為
的距離的比為 。
14分
。
14分
考點:軌跡方程,直線與圓的位置關系
點評:主要是考查了直線與原點位置關系的運用,以及軌跡方程的求解,屬于中檔題。


科目:高中數學 來源:2013屆湖北省武漢市高二下期末理科數學試卷(解析版) 題型:選擇題
已知A,B的坐標分別是 ,直線AM,BM相交于點M,且它們的斜率之和是2,則點M的軌跡方程是( )
,直線AM,BM相交于點M,且它們的斜率之和是2,則點M的軌跡方程是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省蘇北老四所縣中高三(下)第一次調研數學試卷(解析版) 題型:填空題
 則MA+MC= .
則MA+MC= .查看答案和解析>>
科目:高中數學 來源:2011年江蘇省無錫市高考數學模擬試卷(3)(解析版) 題型:解答題
 則MA+MC= .
則MA+MC= .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com