已知函數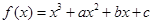
在
與
時都取得極值.
(1)求
的值與函數
的單調區間
(2)若對
，不等式
恒成立，求
的取值范圍．
名校課堂系列答案科目：高中數學 來源： 題型：解答題
已知奇函數 f (x) 在 (－¥,0)∪(0,+¥) 上有意義，且在 (0,+¥) 上是增函數，f (1) = 0，又函數 g(q) = sin 2q+ m cos q－2m，若集合M =" {m" | g(q) < 0}，集合 N =" {m" | f [g(q)] < 0}，求M∩N.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知橢圓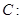
的左焦點為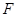
,左、右頂點分別為
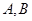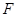,過點且傾斜角為
的直線
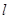交橢圓于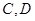
兩點,橢圓
的離心率為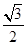
,
．
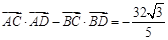（1）求橢圓的方程；
（2）若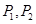
是橢圓上不同兩點，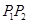
軸，圓
過點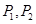，且橢圓上任意一點都不在圓內，則稱圓為該橢圓的內切圓．問橢圓是否存在過點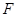的內切圓？若存在，求出點的坐標；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某公司承建扇環面形狀的花壇如圖所示，該扇環面花壇是由以點
為圓心的兩個同心圓弧
、弧
以及兩條線段
和
圍成的封閉圖形．花壇設計周長為30米，其中大圓弧所在圓的半徑為10米．設小圓弧所在圓的半徑為
米（
），圓心角為
弧度．
（1）求關于的函數關系式；
（2）在對花壇的邊緣進行裝飾時，已知兩條線段的裝飾費用為4元/米，兩條弧線部分的裝飾費用為9元/米．設花壇的面積與裝飾總費用的比為
，當為何值時，取得最大值？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某通訊公司需要在三角形地帶
區域內建造甲、乙兩種通信信號加強中轉站，甲中轉站建在區域
內，乙中轉站建在區域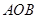
內．分界線
固定，且=
百米，邊界線
始終過點
，邊界線
滿足
．
設
(
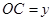)百米，
百米.
(1)試將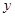
表示成
的函數，并求出函數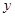的解析式；
(2)當取何值時？整個中轉站的占地面積
最小，并求出其面積的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，函數
與
,遞減區間是
；（2）
或
.
，進而得到
，從中解方程組即可得到
求出函數
求出函數
，從而目標轉向函數
的最大值，進而求解不等式
，
得
，函數
，在
處取最小值．
的值；
中，
分別是
的對邊，已知
,求角
．
的單調性；
時，關于
的方程
有唯一解，求
的值；
時，證明: 對一切
，都有
成立．
，
.
的最小正周期和值域；
，且
，求
的值.
－4
＋2的最大值和最小值．