解:(1)證:∵

=

(
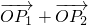
),
∴P是P
1P
2的中點(diǎn)?x
1+x
2=1------(2分)
∴y
1+y
2=f(x
1)+f(x
2)=
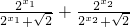
=
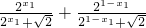
=
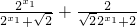
=1.
∴
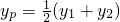
=

..-----------------------------(4分)
(2)解:由(1)知x
1+x
2=1,f (x
1)+f (x
2)=y
1+y
2=1,f (1)=2-

,
S
n=f(

)+f(

)+…+f(

)+f(
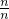
),
S
n=f(
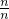
)+f(

)+…+f(

)+f(

),
相加得 2S
n=f(1)+[f(

)+f(

)]+[f(

)+f(
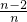
)]+…+[f(

)+f(

)]+f(1),
=2f(1)+n-1=n+3-2

∴
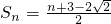
.------------(8分)
(3)解:
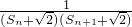
=
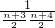
=
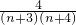
=
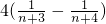
,
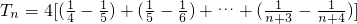
--------------------(10分)
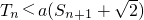
?a
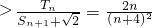
=
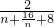
∵
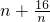
≥8,當(dāng)且僅當(dāng)n=4時(shí),取“=”
∴
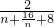
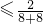
=

,因此,a
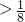
-------------------(12分)
分析:(1)由于點(diǎn)在函數(shù)圖象上,同時(shí)滿足

=

(
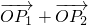
),那么利用坐標(biāo)化簡(jiǎn)得到結(jié)論.
(2)根據(jù)f (x
1)+f (x
2)=y
1+y
2=1,f (1)=2-

,結(jié)合倒序相加法求解得到結(jié)論.
(3)根據(jù)已知的和式得到
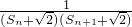
=
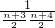
=
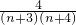
=
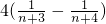
,裂項(xiàng)求和的數(shù)學(xué)思想得到證明.
點(diǎn)評(píng):本試題主要考查了函數(shù),與向量,以及數(shù)列的知識(shí)的綜合運(yùn)用.以函數(shù)為模型,確定點(diǎn)的坐標(biāo)關(guān)系式,進(jìn)一步結(jié)合向量得到結(jié)論,并利用倒序相加法求解和,同時(shí)利用裂項(xiàng)求和得到不等式的證明.

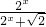 的圖象上兩點(diǎn)P1(x1,y1)、P2(x2,y2),若
的圖象上兩點(diǎn)P1(x1,y1)、P2(x2,y2),若 =
= (
(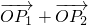 ),且點(diǎn)P的橫坐標(biāo)為
),且點(diǎn)P的橫坐標(biāo)為 .
. )+f(
)+f( )+A+f(
)+A+f( )+f(
)+f(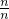 )
)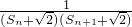 }的前n項(xiàng)和,若Tn<a(Sn+1+
}的前n項(xiàng)和,若Tn<a(Sn+1+ )對(duì)一切n∈N*都成立,試求a的取值范圍.
)對(duì)一切n∈N*都成立,試求a的取值范圍. =
= (
(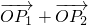 ),
),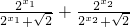 =
=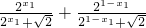 =
=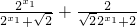 =1.
=1.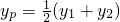 =
= ..-----------------------------(4分)
..-----------------------------(4分) ,
, )+f(
)+f( )+…+f(
)+…+f( )+f(
)+f(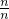 ),
),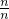 )+f(
)+f( )+…+f(
)+…+f( )+f(
)+f( ),
), )+f(
)+f( )]+[f(
)]+[f( )+f(
)+f(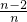 )]+…+[f(
)]+…+[f( )+f(
)+f( )]+f(1),
)]+f(1),
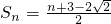 .------------(8分)
.------------(8分)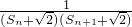 =
=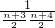 =
=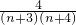 =
=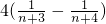 ,
,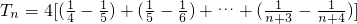 --------------------(10分)
--------------------(10分) 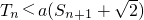 ?a
?a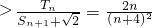 =
=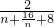
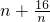 ≥8,當(dāng)且僅當(dāng)n=4時(shí),取“=”
≥8,當(dāng)且僅當(dāng)n=4時(shí),取“=”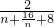
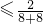 =
= ,因此,a
,因此,a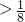 -------------------(12分)
-------------------(12分) =
= (
(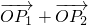 ),那么利用坐標(biāo)化簡(jiǎn)得到結(jié)論.
),那么利用坐標(biāo)化簡(jiǎn)得到結(jié)論. ,結(jié)合倒序相加法求解得到結(jié)論.
,結(jié)合倒序相加法求解得到結(jié)論.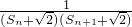 =
=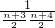 =
=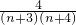 =
=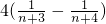 ,裂項(xiàng)求和的數(shù)學(xué)思想得到證明.
,裂項(xiàng)求和的數(shù)學(xué)思想得到證明.

 高中必刷題系列答案
高中必刷題系列答案