
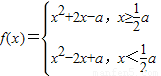 然后根據a>2再結合一元二次函數的單調性可求出f(x)在各段的最小值然后比較兩個最小值的大小則較小的最小值即為所求.
然后根據a>2再結合一元二次函數的單調性可求出f(x)在各段的最小值然后比較兩個最小值的大小則較小的最小值即為所求.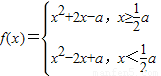
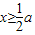 時,f(x)=x2+2x-a=(x+1)2-(a+1)
時,f(x)=x2+2x-a=(x+1)2-(a+1)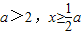 ,得x>1,從而x>-1
,得x>1,從而x>-1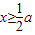 時單調遞增,f(x)的最小值為
時單調遞增,f(x)的最小值為
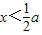 時,f(x)=x2-2x+a=(x-1)2+(a-1)
時,f(x)=x2-2x+a=(x-1)2+(a-1)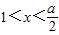 時,f(x)單調遞增,當x<1時,f(x)單調遞減
時,f(x)單調遞增,當x<1時,f(x)單調遞減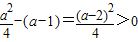 ,知f(x)的最小值為a-1.
,知f(x)的最小值為a-1.

科目:高中數學 來源: 題型:
| 1 | x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| n+1 |
| n |
| n-1 |
| n3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com