
已知函數(shù)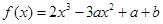 (其中a,b為實常數(shù))。
(其中a,b為實常數(shù))。
(Ⅰ)討論函數(shù)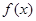 的單調(diào)區(qū)間:
的單調(diào)區(qū)間:
(Ⅱ)當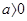 時,函數(shù)
時,函數(shù)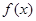 有三個不同的零點,證明:
有三個不同的零點,證明: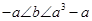 :
:
(Ⅲ)若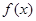 在區(qū)間
在區(qū)間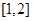 上是減函數(shù),設關于x的方程
上是減函數(shù),設關于x的方程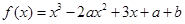 的兩個非零實數(shù)根為
的兩個非零實數(shù)根為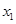 ,
,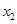 。試問是否存在實數(shù)m,使得
。試問是否存在實數(shù)m,使得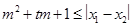 對任意滿足條件的a及t
對任意滿足條件的a及t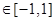 恒成立?若存在,求m的取值范圍;若不存在,請說明理由。
恒成立?若存在,求m的取值范圍;若不存在,請說明理由。
(I)當a=0時,f(x)的增區(qū)間為(-∞,+∞);
當a>0時,f(x)的增區(qū)間為(-∞,0),(a,+∞);f(x)的減區(qū)間為(0,a);
當a<0時,f(x)的增區(qū)間為(-∞,a),(0,+∞);f(x)的減區(qū)間為(a,0).
(II)-a<b<a3-a.(III)存在實數(shù)m滿足條件,此時m∈[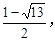
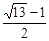 ].
].
解析試題分析:(I)求導函數(shù),對參數(shù)a進行討論,利用導數(shù)的正負,確定函數(shù)的單調(diào)區(qū)間;
(II)確定f(x)的極大值為f(0)=a+b,f(x)的極小值為f(a)=a+b-a3,要使f(x)有三個不同的零點,則f(0)>0,f(a)<0,從而得證;
(III)先確定|x1-x2|=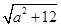 ,并求得其最小值,假設存在實數(shù)m滿足條件,則m2+tm+1≤(
,并求得其最小值,假設存在實數(shù)m滿足條件,則m2+tm+1≤(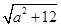 )min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,從而可求m的范圍.
)min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,從而可求m的范圍.
解:(I)∵ 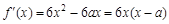 ,
,
當a=0時, ≥0,于是
≥0,于是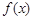 在R上單調(diào)遞增;
在R上單調(diào)遞增;
當a>0時,x∈(0,a),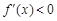 ,得
,得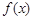 在(0,a)上單調(diào)遞減;
在(0,a)上單調(diào)遞減;
x∈(-∞,0)∪(a,+∞),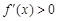 ,得
,得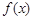 在(-∞,0),(a,+∞)上單調(diào)遞增;
在(-∞,0),(a,+∞)上單調(diào)遞增;
當a<0時,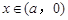 ,
,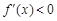 ,得
,得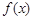 在(0,a)上單調(diào)遞減;
在(0,a)上單調(diào)遞減;
x∈(-∞,a)∪(0,+∞),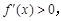 得
得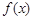 在(-∞,a),(0,+∞)上單調(diào)遞增.
在(-∞,a),(0,+∞)上單調(diào)遞增.
綜上所述:當a=0時,f(x)的增區(qū)間為(-∞,+∞);
當a>0時,f(x)的增區(qū)間為(-∞,0),(a,+∞);f(x)的減區(qū)間為(0,a);
當a<0時,f(x)的增區(qū)間為(-∞,a),(0,+∞);f(x)的減區(qū)間為(a,0).……3分
(II)當a>0時,由(I)得f(x)在(-∞,0),(a,+∞)上是增函數(shù),f(x)在(0,a)上是減函數(shù);則f(x)的極大值為f(0)=a+b,f(x)的極小值為f(a)=a+b-a3.
要使f(x)有三個不同的零點,則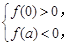 即
即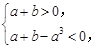 可得-a<b<a3-a.…8分
可得-a<b<a3-a.…8分
(III)由2x3-3ax2+a+b=x3-2ax2+3x+a+b,得x3-ax2-3x=0即x(x2-ax-3)=0,
由題意得x2-ax-3=0有兩非零實數(shù)根x1,x2,則x1+x2=a,x1x2=-3,
即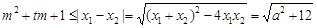 .∵ f (x)在[1,2]上是減函數(shù),
.∵ f (x)在[1,2]上是減函數(shù),
∴ 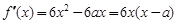 ≤0在[1,2]上恒成立,
≤0在[1,2]上恒成立,
其中x-a≤0即x≤a在[1,2]上恒成立,∴ a≥2.∴ 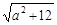 ≥4.
≥4.
假設存在實數(shù)m滿足條件,則m2+tm+1≤(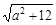 )min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,
)min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,
∴ 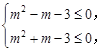 解得
解得 .
.
∴ 存在實數(shù)m滿足條件,此時m∈[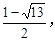
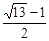 ]. …………………14分
]. …………………14分
考點:本題主要考查導數(shù)知識的運用,考查函數(shù)的單調(diào)性,考查分類討論的數(shù)學思想,考查函數(shù)的極值與最值,考查恒成立問題,綜合性強.
點評:解決該試題的關鍵是利用導數(shù)的正負對于函數(shù)單調(diào)性的影響得到函數(shù)單調(diào)區(qū)間,進而分析極值問題,以及構造函數(shù)的思想求證函數(shù)的最值,解決恒成立問題的運用。


科目:高中數(shù)學 來源: 題型:解答題
某工廠每天生產(chǎn)某種產(chǎn)品最多不超過40件,并且在生產(chǎn)過程中產(chǎn)品的正品率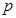 與每日生產(chǎn)產(chǎn)品件數(shù)
與每日生產(chǎn)產(chǎn)品件數(shù)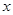 (
(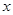

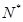 )間的關系為
)間的關系為 ,每生產(chǎn)一件正品盈利4000元,每出現(xiàn)一件次品虧損2000元.
,每生產(chǎn)一件正品盈利4000元,每出現(xiàn)一件次品虧損2000元.
(注:正品率=產(chǎn)品的正品件數(shù)÷產(chǎn)品總件數(shù)×100%)
(1)將日利潤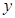 (元)表示成日產(chǎn)量
(元)表示成日產(chǎn)量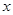 (件)的函數(shù);
(件)的函數(shù);
(2)求該廠的日產(chǎn)量為多少件時,日利潤最大?并求出日利潤的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
( 本題滿分14分) 提高過江大橋的車輛通行能力可改善整個城市的交通狀況。在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度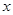 (單位:輛/千米)的函數(shù)。當橋上的的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明;當2
(單位:輛/千米)的函數(shù)。當橋上的的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明;當2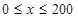 時,車流速度v是車流密度x的一次函數(shù).
時,車流速度v是車流密度x的一次函數(shù).
(Ⅰ)當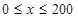 時,求函數(shù)
時,求函數(shù)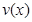 的表達式;
的表達式;
(Ⅱ)當車流密度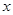 為多大時,車流量(單位時間內(nèi)通過橋上某觀測點的車輛數(shù),單位:輛/每小時)
為多大時,車流量(單位時間內(nèi)通過橋上某觀測點的車輛數(shù),單位:輛/每小時)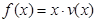 可以達到最大,并求出最大值(精確到1輛/小時).
可以達到最大,并求出最大值(精確到1輛/小時).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本題滿分12分)已知函數(shù) 在點
在點 處取得極小值-4,使其導函數(shù)
處取得極小值-4,使其導函數(shù)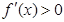 的
的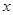 的取值范圍為(1,3)
的取值范圍為(1,3)
(Ⅰ)求 的解析式及
的解析式及 的極大值;
的極大值;
(Ⅱ)當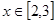 時,求
時,求 的最大值。
的最大值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
小王需不定期地在某超市購買同一品種的大米.現(xiàn)有甲、乙兩種不同的采購策略,策略甲:每次購買大米的數(shù)量一定;策略乙:每次購買大米的錢數(shù)一定.若以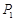 (元)和
(元)和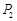 (元)分別記小王先后兩次買米時,該品種大米的單價,請問:僅這兩次買米而言,甲、乙兩種購買方式,從平均單價考慮,哪種比較合算?請進行探討,并給出探討過程.
(元)分別記小王先后兩次買米時,該品種大米的單價,請問:僅這兩次買米而言,甲、乙兩種購買方式,從平均單價考慮,哪種比較合算?請進行探討,并給出探討過程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)f(x)=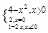
(1)求f(f(-2))的值;
(2)求f(a2+1)(a∈R)的值;
(3)當-4≤x<3時,求函數(shù)f(x)的值域.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本題滿分13分)已知函數(shù)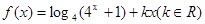 是偶函數(shù)
是偶函數(shù)
(1)求k的值;
(2)設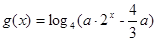 ,若函數(shù)f(x)與g(x)的圖像有且只有一個公共點,求實數(shù)a的取值范圍。
,若函數(shù)f(x)與g(x)的圖像有且只有一個公共點,求實數(shù)a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)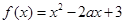
(1)若函數(shù)在 的單調(diào)遞減區(qū)間(—∞,2],求函數(shù)
的單調(diào)遞減區(qū)間(—∞,2],求函數(shù) 在區(qū)間[3,5]上的最大值.
在區(qū)間[3,5]上的最大值.
(2)若函數(shù)在 在單區(qū)間(—∞,2]上是單調(diào)遞減,求函數(shù)
在單區(qū)間(—∞,2]上是單調(diào)遞減,求函數(shù)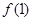 的最大值.
的最大值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com