
(本題滿分16分)已知函數(shù) (其中
(其中 為常數(shù),
為常數(shù), )為偶函數(shù).
)為偶函數(shù).
(1) 求 的值;
的值;
(2) 用定義證明函數(shù) 在
在 上是單調(diào)減函數(shù);
上是單調(diào)減函數(shù);
(3) 如果 ,求實數(shù)
,求實數(shù) 的取值范圍.
的取值范圍.
(1)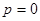 ;(2)見解析;(3)
;(2)見解析;(3)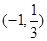
【解析】
試題分析:(1) 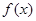 是偶函數(shù)有
是偶函數(shù)有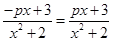 即
即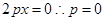 .…………4分
.…………4分
(2)由(1)  . 設(shè)
. 設(shè) , ………………6分
, ………………6分
則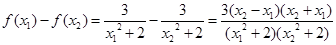 . ……………………8分
. ……………………8分

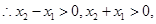
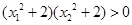 .
.

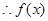 在
在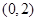 上是單調(diào)減函數(shù). ……………………10分
上是單調(diào)減函數(shù). ……………………10分
(3)由(2)得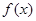 在
在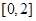 上為減函數(shù),又
上為減函數(shù),又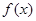 是偶函數(shù),所以
是偶函數(shù),所以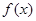 在
在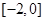 上為單調(diào)增函數(shù).
……………………………………………12分
上為單調(diào)增函數(shù).
……………………………………………12分
不等式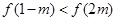 即
即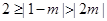 ,4>
,4> .
.
解得 . 所以實數(shù)
. 所以實數(shù) 的取值范圍是
的取值范圍是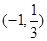 .…………………16分
.…………………16分
說明(3)如果是分情況討論,知道分類給2分.并做對一部分則再給2分.
考點:函數(shù)的奇偶性;函數(shù)的單調(diào)性;利用函數(shù)的奇偶性和單調(diào)性解不等式。
點評:解這類 不等式,關(guān)鍵是利用函數(shù)的奇偶性和它在定義域內(nèi)的單調(diào)性,去掉“f”符號,轉(zhuǎn)化為代數(shù)不等式組求解,但要特別注意函數(shù)定義域的作用。
不等式,關(guān)鍵是利用函數(shù)的奇偶性和它在定義域內(nèi)的單調(diào)性,去掉“f”符號,轉(zhuǎn)化為代數(shù)不等式組求解,但要特別注意函數(shù)定義域的作用。


科目:高中數(shù)學(xué) 來源:2010-2011年江蘇省淮安市楚州中學(xué)高二上學(xué)期期末考試數(shù)學(xué)試卷 題型:解答題
(本題滿分16分)
已知函數(shù) ,且對任意
,且對任意 ,有
,有 .
.
(1)求 ;
;
(2)已知 在區(qū)間(0,1)上為單調(diào)函數(shù),求實
在區(qū)間(0,1)上為單調(diào)函數(shù),求實 數(shù)
數(shù)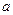 的取值范圍.
的取值范圍.
(3)討論函數(shù) 的零點個數(shù)?(提示
的零點個數(shù)?(提示 :
: )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年浙江省高三10月階段性測試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分16分)已知函數(shù) 為實常數(shù)).
為實常數(shù)).
(I)當(dāng) 時,求函數(shù)
時,求函數(shù) 在
在 上的最小值;
上的最小值;
(Ⅱ)若方程 在區(qū)間
在區(qū)間 上有解,求實數(shù)
上有解,求實數(shù) 的取值范圍;
的取值范圍;
(Ⅲ)證明:
(參考數(shù)據(jù): )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆江蘇省高二下期中理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分16分) 已知橢圓 :
: 的離心率為
的離心率為 ,
, 分別為橢圓
分別為橢圓 的左、右焦點,若橢圓
的左、右焦點,若橢圓 的焦距為2.
的焦距為2.
⑴求橢圓 的方程;
的方程;
⑵設(shè) 為橢圓上任意一點,以
為橢圓上任意一點,以 為圓心,
為圓心, 為半徑作圓
為半徑作圓 ,當(dāng)圓
,當(dāng)圓 與橢圓的右準(zhǔn)線
與橢圓的右準(zhǔn)線 有公共點時,求△
有公共點時,求△ 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆江蘇省高一上學(xué)期期中考試數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分16分)已知函數(shù) 是定義在
是定義在 上的偶函數(shù),且當(dāng)
上的偶函數(shù),且當(dāng) 時,
時, 。
。
(Ⅰ)求 及
及 的值;
的值;
(Ⅱ)求函數(shù) 在
在 上的解析式;
上的解析式;
(Ⅲ)若關(guān)于 的方程
的方程 有四個不同的實數(shù)解,求實數(shù)
有四個不同的實數(shù)解,求實數(shù) 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:江蘇省2009-2010學(xué)年高二第二學(xué)期期末考試 題型:解答題
本題滿分16分)已知圓內(nèi)接四邊形ABCD的邊長分別為AB = 2,BC = 6,CD = DA = 4 ;求四邊形ABCD的面積.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com