
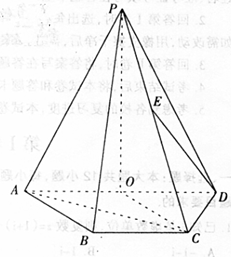
如圖,四棱錐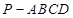 中,底面
中,底面 是直角梯形,
是直角梯形,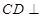 平面
平面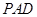 ,
,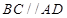 ,
,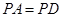 ,
,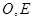 分別為
分別為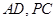 的中點(diǎn),
的中點(diǎn),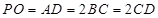 .
.
(1)求證: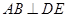 ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)證明過程詳見解析;(2)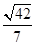 .
.
解析試題分析:本題主要以四棱錐為幾何背景考查線線垂直、線線平行、面面垂直、線面垂直和二面角的求法,可以運(yùn)用傳統(tǒng)幾何法,也可以運(yùn)用空間向量法求解,突出考查空間想象能力和計(jì)算能力.方法一:第一問,由于四邊形 為正方形,所以
為正方形,所以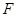 是
是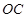 中點(diǎn),在
中點(diǎn),在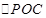 中,利用中位線得
中,利用中位線得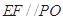 ,利用面面垂直的判定得平面
,利用面面垂直的判定得平面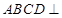 平面
平面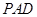 ,在
,在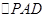 中,由已知得
中,由已知得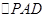 為等腰三角形,而
為等腰三角形,而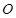 是
是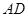 的中點(diǎn),所以得
的中點(diǎn),所以得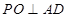 ,所以得
,所以得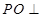 平面
平面 ,而
,而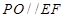 ,所以
,所以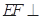 平面
平面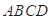 ,所以
,所以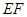 垂直面
垂直面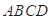 內(nèi)的線
內(nèi)的線 ,在
,在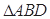 中,利用勾股定理得,
中,利用勾股定理得,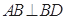 ,所以利用線面垂直的判定得
,所以利用線面垂直的判定得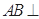 平面
平面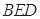 ,所以
,所以 垂直面
垂直面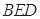 內(nèi)的線
內(nèi)的線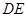 ;第二問,由線面垂直
;第二問,由線面垂直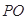
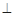 平面
平面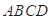 ,得面面垂直平面
,得面面垂直平面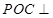 平面
平面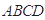 ,由
,由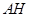 垂直兩個(gè)面的交線,所以
垂直兩個(gè)面的交線,所以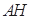
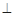 平面
平面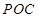 ,所以
,所以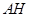 垂直面內(nèi)的線
垂直面內(nèi)的線 ,在等腰三角形
,在等腰三角形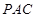 中,
中,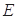 是
是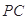 中點(diǎn),所以
中點(diǎn),所以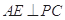 ,從而得
,從而得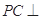 平面
平面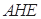 ,所以
,所以 垂直面內(nèi)的線
垂直面內(nèi)的線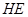 ,從而得
,從而得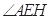 是二面角
是二面角 的平面角,由已知中的邊的關(guān)系得出
的平面角,由已知中的邊的關(guān)系得出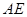 、
、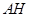 的長(zhǎng)度,從而得出
的長(zhǎng)度,從而得出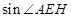 的值,再利用平方關(guān)系得出角的余弦值;方法二:第一問,利用向量法,先建立空間直角坐標(biāo)系,寫出各個(gè)點(diǎn)的坐標(biāo)及向量的坐標(biāo),要證明
的值,再利用平方關(guān)系得出角的余弦值;方法二:第一問,利用向量法,先建立空間直角坐標(biāo)系,寫出各個(gè)點(diǎn)的坐標(biāo)及向量的坐標(biāo),要證明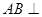
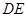 ,只需證明
,只需證明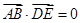 即可;第二問,利用向量法求出面
即可;第二問,利用向量法求出面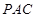 的法向量,面
的法向量,面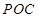 的法向量,再利用夾角公式求余弦值.
的法向量,再利用夾角公式求余弦值.
試題解析:解法一:(Ⅰ)設(shè)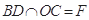 ,連接
,連接 ,
,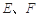 分別是
分別是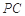 、
、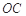 的中點(diǎn),則
的中點(diǎn),則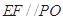 , 1分
, 1分
已知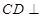 平面
平面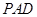 ,
,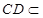 平面
平面 ,所以平面
,所以平面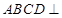 平面
平面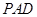 ,
,
又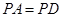 ,
,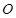 為
為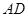 的中點(diǎn),則
的中點(diǎn),則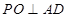 ,
,
而平面


 百年學(xué)典課時(shí)學(xué)練測(cè)系列答案
百年學(xué)典課時(shí)學(xué)練測(cè)系列答案 仁愛英語同步練習(xí)冊(cè)系列答案
仁愛英語同步練習(xí)冊(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,四邊形 是正方形,
是正方形, 平面
平面 ,
,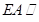
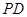 ,
,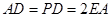 ,
,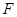 ,
,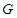 ,
, 分別為
分別為 ,
,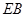 ,
, 的中點(diǎn).
的中點(diǎn).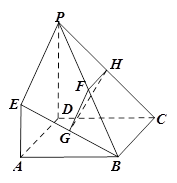
(1)求證: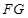
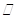 平面
平面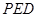 ;
;
(2)求平面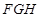 與平面
與平面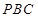 所成銳二面角的大小.
所成銳二面角的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,長(zhǎng)方體 中,
中,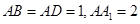 ,點(diǎn)
,點(diǎn) 為
為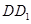 的中點(diǎn).
的中點(diǎn).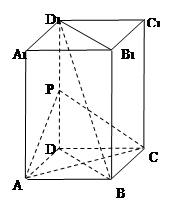
(1)求證:直線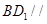 平面
平面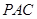 ;
;
(2)求證:平面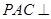 平面
平面 ;
;
(3)求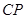 與平面
與平面 所成的角大小.
所成的角大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,點(diǎn)D是AB的中點(diǎn).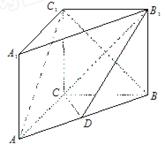
(1)求證: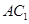 ∥平面
∥平面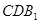 ;
;
(2)求證:AC⊥BC1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖長(zhǎng)方體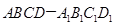 中,底面
中,底面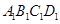 是正方形,
是正方形,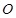 是
是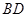 的中點(diǎn),
的中點(diǎn),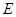 是棱
是棱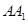 上任意一點(diǎn).
上任意一點(diǎn).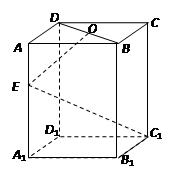
⑴求證: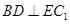 ;
;
⑵如果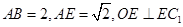 ,求
,求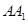 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com