
隨著經濟的發展,人們生活水平的提高,中學生的營養與健康問題越來越得到學校與家長的重視. 從學生體檢評價報告單了解到某校3000名學生的體重發育評價情況,得右表:
| | 偏瘦 | 正常 | 肥胖 |
| 女生(人) | 300 | 865 |  |
| 男生(人) | 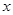 | 885 | 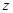 |
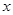 的值;
的值;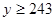 ,
,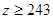 ,求肥胖學生中男生不少于女生的概率.
,求肥胖學生中男生不少于女生的概率. (Ⅰ)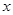 =450;(Ⅱ)應在肥胖學生中抽10名;(Ⅲ)
=450;(Ⅱ)應在肥胖學生中抽10名;(Ⅲ)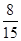 .
.
解析試題分析:(Ⅰ)利用“從3000名學生中隨機抽取1名學生,抽到偏瘦男生的概率為0.15”可求得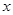 ;(Ⅱ)根據分層抽樣可求;(Ⅲ)利用古典概型求解.
;(Ⅱ)根據分層抽樣可求;(Ⅲ)利用古典概型求解.
試題解析:(Ⅰ)由題意可知 , ∴
, ∴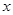 =450(人) 3分
=450(人) 3分
(Ⅱ)由題意知,肥胖學生人數為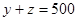 (人)。 設應在肥胖學生中抽取
(人)。 設應在肥胖學生中抽取 人,
人,
則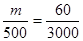 , ∴
, ∴ (人) 答:應在肥胖學生中抽10名 6分
(人) 答:應在肥胖學生中抽10名 6分
(Ⅲ)由題意可知, 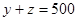 ,且
,且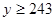 ,
,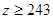 ,滿足條件的
,滿足條件的
( ,
,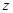 )有(243,257),(244,256), ,(257,243),共有15組。
)有(243,257),(244,256), ,(257,243),共有15組。
設事件A:“肥胖學生中男生不少于女生”,即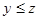 ,滿足條件的(
,滿足條件的( ,
,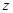 )
)
(243,257),(244,256), ,(250,250),共有8組,所以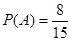 。
。
答:肥胖學生中男生不少于女生的概率為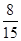 12分
12分
考點:分層抽樣,古典概率.


科目:高中數學 來源: 題型:解答題
一個口袋中有紅球3個,白球4個.
(Ⅰ)從中不放回地摸球,每次摸2個,摸到的2個球中至少有1個紅球則中獎,求摸2次恰好第2次中獎的概率;
(Ⅱ)每次同時摸2個,并放回,摸到的2個球中至少有1個紅球則中獎,連續摸4次,求中獎次數X的數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校學習小組開展“學生語文成績與外語成績的關系”的課題研究,對該校高二年級800名學生上學期期末語文和外語成績,按優秀和不優秀分類得結果:語文和外語都優秀的有60人,語文成績優秀但外語不優秀的有140人,外語成績優秀但語文不優秀的有100人.
(Ⅰ)能否在犯錯概率不超過0.001的前提下認為該校學生的語文成績與外語成績有關系?
(Ⅱ)4名成員隨機分成兩組,每組2人,一組負責收集成績,另一組負責數據處理。求學生甲分到負責收集成績組,學生乙分到負責數據處理組的概率。
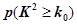 | 0.010 | 0.005 | 0.001 |
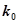 | 6.635 | 7.879 | 10.828 |
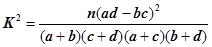
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某超市在節日期間進行有獎促銷,凡在該超市購物滿300元的顧客,將獲得一次摸獎機會,規則如下:獎盒中放有除顏色外完全相同的1個紅球,1個黃球,1個白球和1個黑球.顧客不放回的每次摸出1個球,若摸到黑球則停止摸獎,否則就要將獎盒中的球全部摸出才停止.規定摸到紅球獎勵10元,摸到白球或黃球獎勵5元,摸到黑球不獎勵.
(Ⅰ)求1名顧客摸球3次停止摸獎的概率;
(Ⅱ)記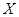 為1名顧客摸獎獲得的獎金數額,求隨機變量
為1名顧客摸獎獲得的獎金數額,求隨機變量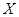 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個口袋中有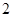 個白球和
個白球和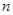 個紅球
個紅球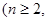 且
且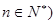 ,每次從袋中摸出兩個球(每次摸球后把這兩個球放回袋中),若摸出的兩個球顏色相同為中獎,否則為不中獎.
,每次從袋中摸出兩個球(每次摸球后把這兩個球放回袋中),若摸出的兩個球顏色相同為中獎,否則為不中獎.
(Ⅰ)試用含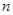 的代數式表示一次摸球中獎的概率
的代數式表示一次摸球中獎的概率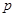 ;
;
(Ⅱ)若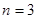 ,求三次摸球恰有一次中獎的概率;
,求三次摸球恰有一次中獎的概率;
(Ⅲ)記三次摸球恰有一次中獎的概率為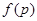 ,當
,當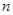 為何值時,
為何值時,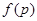 取最大值.
取最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某社團組織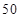 名志愿者利用周末和節假日參加社會公益活動,活動內容是:1、到各社區宣傳慰問,倡導文明新風;2、到指定的醫院、福利院做義工,幫助那些需要幫助的人.各位志愿者根據各自的實際情況,選擇了不同的活動項目,相關的數據如下表所示:
名志愿者利用周末和節假日參加社會公益活動,活動內容是:1、到各社區宣傳慰問,倡導文明新風;2、到指定的醫院、福利院做義工,幫助那些需要幫助的人.各位志愿者根據各自的實際情況,選擇了不同的活動項目,相關的數據如下表所示:
| | 宣傳慰問 | 義工 | 總計 |
| 20至40歲 | 11 | 16 | 27 |
| 大于40歲 | 15 | 8 | 23 |
| 總計 | 26 | 24 | 50 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為增強市民的節能環保意識,某市面向全市征召義務宣傳志愿者.從符合條件的500名志愿者中隨機抽取100名志愿者,其年齡頻率分布直方圖如圖所示,其中年齡分組區間是: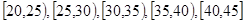 .
.
(I)求圖中 的值并根據頻率分布直方圖估計這500名志愿者中年齡在
的值并根據頻率分布直方圖估計這500名志愿者中年齡在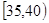 歲的人數;
歲的人數;
(II)在抽出的100名志愿者中按年齡采用分層抽樣的方法抽取20名參加中心廣場的宣傳活動,再從這20名中采用簡單隨機抽樣方法選取3名志愿者擔任主要負責人.記這3名志愿者中“年齡低于35歲”的人數為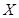 ,求
,求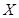 的分布列及數學期望.
的分布列及數學期望. 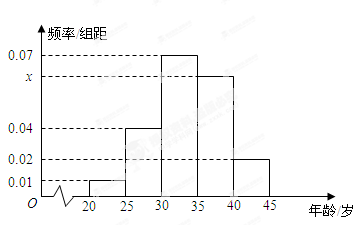
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某聯歡晚會舉行抽獎活動,舉辦方設置了甲.乙兩種抽獎方案,方案甲的中獎率為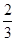 ,中將可以獲得2分;方案乙的中獎率為
,中將可以獲得2分;方案乙的中獎率為 ,中將可以得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中將與否互不影響,晚會結束后憑分數兌換獎品.
,中將可以得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中將與否互不影響,晚會結束后憑分數兌換獎品.
(1)若小明選擇方案甲抽獎,小紅選擇方案乙抽獎,記他們的累計得分為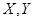 ,求
,求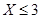 的概率;
的概率;
(2)若小明.小紅兩人都選擇方案甲或方案乙進行抽獎,問:他們選擇何種方案抽獎,累計的得分的數學期望較大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
2013年3月2日,國家環保部發布了新修訂的《環境空氣質量標準》.其中規定:居民區的PM2.5年平均濃度不得超過35微克/立方米,PM2.5的24小時平均濃度不得超過75微克/立方米. 某城市環保部門隨機抽取了一居民區去年20天PM2.5的24小時平均濃度的監測數據,數據統計如下:
| 組別 | PM2.5濃度 (微克/立方米) | 頻數(天) | 頻率 |
| 第一組 | (0,25] | 5 | 0.25 |
| 第二組 | (25,50] | 10 | 0.5 |
| 第三組 | (50,75] | 3 | 0.15 |
| 第四組 | (75,100) | 2 | 0.1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com