
某商場銷售某種商品的經驗表明,該商品每日的銷售量y(單位:千克)與銷售價格x(單位:元/千克)滿足關系式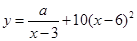 ,其中3<x<6,a 為常數,已知銷售價格為5元/千克時,每日可售出該商品11千克。
,其中3<x<6,a 為常數,已知銷售價格為5元/千克時,每日可售出該商品11千克。
(I)求a的值
(II)若該商品的成品為3元/千克,試確定銷售價格x的值,使商場每日銷售該商品所獲得的利潤最大。
科目:高中數學 來源: 題型:解答題
規定 其中
其中 ,
, 為正整數,且
為正整數,且 =1,這是排列數
=1,這是排列數 (
( 是正整數,
是正整數, )的一種推廣.
)的一種推廣.
(Ⅰ) 求 的值;
的值;
(Ⅱ)排列數的兩個性質:①
 ,②
,②

 (其中m,n是正整數).是否都能推廣到
(其中m,n是正整數).是否都能推廣到 (
( ,
, 是正整數)的情形?若能推廣,寫出推廣的形式并給予證明;若不能,則說明理由;
是正整數)的情形?若能推廣,寫出推廣的形式并給予證明;若不能,則說明理由;
(Ⅲ)已知函數 ,試討論函數
,試討論函數 的零點個數.
的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數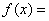
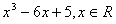 .
.
(1)求函數 的單調區間和極值。
的單調區間和極值。
(2)若關于 的方程
的方程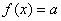 有三個不同實根,求實數
有三個不同實根,求實數 的取值范圍;
的取值范圍;
(3)已知當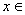 (1,+∞)時,
(1,+∞)時,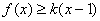 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com