
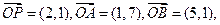 設
設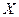 是直線
是直線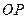 上的一點, (其中
上的一點, (其中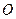 為坐標原點).
為坐標原點).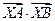 取最小值時的點
取最小值時的點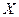 的坐標和此時
的坐標和此時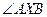 的余弦值.
的余弦值. 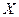 .若
.若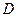 是線段
是線段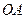 的三等分點,且
的三等分點,且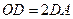 ,
,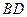 與
與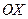 交于點
交于點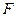 ,設
,設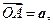
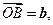 試用
試用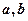 表示
表示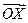 和
和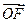 .
. 
 小題狂做系列答案
小題狂做系列答案科目:高中數學 來源:不詳 題型:解答題
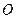 為坐標原點,
為坐標原點,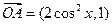 ,
,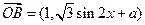 (
(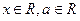 ,
,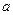 是常數),若
是常數),若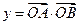
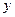 關于
關于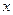 的函數關系式
的函數關系式 ;
;  的最大值為
的最大值為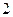 ,求
,求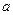 的值;
的值;  單調區間。
單調區間。查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
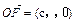 (c>0),
(c>0),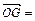 (n, n)(n∈R),
(n, n)(n∈R), 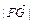 的最小值為1,若動點P同時滿足下列三個條件:①
的最小值為1,若動點P同時滿足下列三個條件:①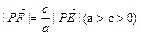 ,②
,②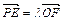 (其中
(其中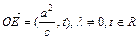 );③動點P的軌跡C經過點B(0,-1)。
);③動點P的軌跡C經過點B(0,-1)。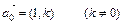 的直線l與曲線C交于不同兩點M、N,若
的直線l與曲線C交于不同兩點M、N,若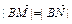 ,求k的取值范圍。
,求k的取值范圍。查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| PM |
| 1 |
| 2 |
| MP′ |
| 5 |
| 5 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
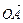 、
、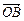 、
、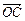 ,其中與
,其中與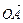 與
與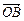 的夾角為120°,
的夾角為120°,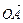 與
與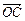 的夾角為30°,且|
的夾角為30°,且|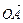 |=|
|=|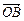 |=1,|
|=1,|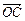 |=
|=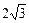 ,若
,若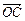 =λ
=λ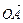 +μ
+μ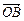 (λ,μ∈R),則λ+μ的值為
(λ,μ∈R),則λ+μ的值為 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com