
如圖,有一塊拋物線形狀的鋼板,計劃將此鋼板切割成等腰梯形ABCD的形狀,使得A,B,C,D都落在拋物線上,點A,B關于拋物線的軸對稱,且AB=2,拋物線的頂點到底邊的距離是2,記CD=2t,梯形面積為S.
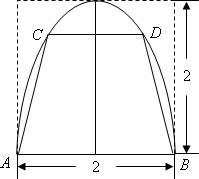
(1)以拋物線的頂點為坐標原點,其對稱軸為y軸建立坐標系,使拋物線開口向下,求出該拋物線的方程;
(2)求面積S關于t的函數解析式,并寫出其定義域;
(3)求面積S的最大值.
 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源: 題型:
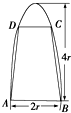 如圖,有一塊拋物線形鋼板,其垂直于對稱軸的邊界線AB長為2r,高為4r,計劃將此鋼板切割成等腰梯形的形狀,以AB為下底,上底CD的端點在拋物線上,記CD=2x,梯形面積為S.求面積S,使其為以x為自變量的函數式,并寫出其定義域.
如圖,有一塊拋物線形鋼板,其垂直于對稱軸的邊界線AB長為2r,高為4r,計劃將此鋼板切割成等腰梯形的形狀,以AB為下底,上底CD的端點在拋物線上,記CD=2x,梯形面積為S.求面積S,使其為以x為自變量的函數式,并寫出其定義域.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com