
 +
+ =1(a>b>0)的左、右兩個焦點.
=1(a>b>0)的左、右兩個焦點. )到F1、F2兩點的距離之和等于4,寫出橢圓C的方程和焦點坐標;
)到F1、F2兩點的距離之和等于4,寫出橢圓C的方程和焦點坐標; ),求|PQ|的最大值;
),求|PQ|的最大值; -
- =1寫出具有類似特性的性質(不必給出證明).
=1寫出具有類似特性的性質(不必給出證明). ),因此
),因此 ,解得b=
,解得b= ,所以c=1,
,所以c=1, ,F1、F2兩焦點坐標為(-1,0),(1,0).
,F1、F2兩焦點坐標為(-1,0),(1,0). ,∴
,∴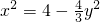 ,Q(0,
,Q(0, ),
),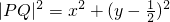 =-
=-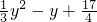 =
=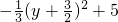 ,
,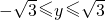 ,
,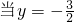 時,|PQ|的最大值=
時,|PQ|的最大值= ;
; -
- =1上關于原點對稱的兩個點,點P在雙曲線上任意一點,當直線PM、PN的斜率都存在,并記為KPM、KPN時,那么KPM與KPN之積是與點P位置無關的定值.
=1上關于原點對稱的兩個點,點P在雙曲線上任意一點,當直線PM、PN的斜率都存在,并記為KPM、KPN時,那么KPM與KPN之積是與點P位置無關的定值. )到F1、F2兩點的距離之和等于4,利用橢圓的定義,求出a,b,c 即可得到橢圓C的方程和焦點坐標;
)到F1、F2兩點的距離之和等于4,利用橢圓的定義,求出a,b,c 即可得到橢圓C的方程和焦點坐標; ),求|PQ|的表達式,結合y的范圍即可求出y的最大值;
),求|PQ|的表達式,結合y的范圍即可求出y的最大值;

科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 (a>b>0)的左、右兩個焦點,橢圓C上的點
(a>b>0)的左、右兩個焦點,橢圓C上的點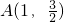 到兩點的距離之和等于4.
到兩點的距離之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com