中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知橢圓長軸上有一點到兩個焦點之間的距離分別為：3＋2，3－2

 （1）求橢圓的方程；

 （2）如果直線x=t(teR）與橢圓相交于A,B，若C（－3,0），D(3,0），證明直線CA與直線

BD的交點K必在一條確定的雙曲線上；

  （3）過點Q(1,0 )作直線l(與x軸不垂直）與橢圓交于M,N兩點，與y軸交于點R，、若

，求證：為定值．

 

【答案】

（1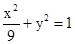）．（2）直線CA與直線BD的交點K必在雙曲線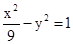上

（3）λ+μ=-．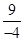

【解析】本試題主要是考查了圓錐曲線方程的求解，以及直線與圓錐曲線的位置關系的綜合運用。

（1）因為橢圓長軸上有一點到兩個焦點之間的距離分別為：3＋2，3－2可知2a=6,a=3,然后結合a,b,c關系的得到橢圓的方程；

（2）因為 直線x=t(teR）與橢圓相交于A,B，若C（－3,0），D(3,0），要證明直線CA與直線BD的交點K必在一條確定的雙曲線上；關鍵是表示出兩條直線方程，然后得到證明。

（3）過點Q(1,0 )作直線l(與x軸不垂直）與橢圓交于M,N兩點，與y軸交于點R，聯立方程組和韋達定理以及向量的關系式得到參數的關系式

 

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

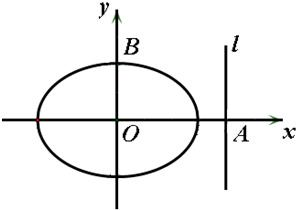精英家教網已知橢圓E：
x2
a2
+
y2
b2
=1(a＞b＞0)的離心率為
2
2
，且過點P(2，
2
)，設橢圓的右準線l與x軸的交點為A，橢圓的上頂點為B，直線AB被以原點為圓心的圓O所截得的弦長為
4
5
5
．
（1）求橢圓E的方程及圓O的方程；
（2）若M是準線l上縱坐標為t的點，求證：存在一個異于M的點Q，對于圓O上任意一點N，有
MN
NQ
為定值；且當M在直線l上運動時，點Q在一個定圓上．

查看答案和解析>>

科目：高中數學 來源： 題型：

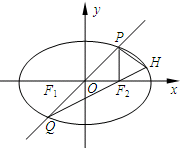已知橢圓
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦點分別為F1，F2．
（Ⅰ）若橢圓的焦距為2
3
，且兩條準線間的距離為
8
3
3
，求橢圓的方程；
（Ⅱ）在（I）的條件下，橢圓上有一點M，滿足MF1⊥MF2，求△MF1F2的面積；
（Ⅲ）過焦點F2作橢圓長軸的垂線與橢圓交于第一象限點P，連接PO并延長交橢圓于點Q，連接QF2并延長交橢圓于點H，若PH⊥PQ，求橢圓的離心率．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2010•廣東模擬）已知橢圓C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的上頂點為A（0，1），過C1的焦點且垂直長軸的弦長軸的弦長為1．
（1）求橢圓C1的方程；
（2）設圓O：x2+y2=
4
5
，過該圓上任意一點作圓的切線l，試證明l和橢圓C1恒有兩個交點A，B，且有
OA
•
OB
=0；
（3）在（2）的條件下求弦AB長度的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

精英家教網已知橢圓的中心在坐標原點，焦點在x軸上，并且焦距為2，短軸與長軸的比是
3
2
．
（1）求橢圓的方程；
（2）已知橢圓中有如下定理：過橢圓
x2
a2
+
y2
b2
=1(a＞b＞0)上任意一點M（x0，y0）的切線唯一，且方程為
x0x
a2
+
y0y
b2
=1，利用此定理求過橢圓的點(1，
3
2
)的切線的方程；
（3）如圖，過橢圓的右準線上一點P，向橢圓引兩條切線PA，PB，切點為A，B，求證：A，F，B三點共線．

查看答案和解析>>

同步練習冊答案