
已知函數 .
.
(1)把 的解析式
的解析式 Acos(
Acos( )+B的形式,并用五點法作出
)+B的形式,并用五點法作出 在一個周期上的簡圖;(要求列表)
在一個周期上的簡圖;(要求列表)
(2)說出 的圖像經過怎樣的變換
的圖像經過怎樣的變換 的圖像.
的圖像.
(1)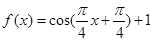 ;(2)
;(2) 的圖像向左平移
的圖像向左平移 個單位得到
個單位得到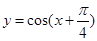 圖像的;縱坐標不變,橫坐標變為原來的
圖像的;縱坐標不變,橫坐標變為原來的 倍得到
倍得到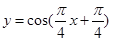 的圖像;向上平移1個單位得到
的圖像;向上平移1個單位得到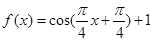 的圖像.
的圖像.
解析試題分析:解題思路:(1)利用二倍角的變形“降次升角”變形即得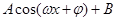 的形式,再利用“列表、描點、連線”法進行作簡圖;(2)利用“平移、伸縮、平移”步驟進行圖像變換.規律總結:三角函數的化簡,即利用同角三角函數基本關系式、誘導公式、兩角和差的三角公式、二倍角公式及其變形化成
的形式,再利用“列表、描點、連線”法進行作簡圖;(2)利用“平移、伸縮、平移”步驟進行圖像變換.規律總結:三角函數的化簡,即利用同角三角函數基本關系式、誘導公式、兩角和差的三角公式、二倍角公式及其變形化成 的形式;三角函數的圖像變換一般兩個途徑:①先左右平移(左加右減),再沿橫坐標軸進行伸縮(
的形式;三角函數的圖像變換一般兩個途徑:①先左右平移(左加右減),再沿橫坐標軸進行伸縮( 縮短,
縮短, 伸長),再沿縱坐標軸進行伸縮(
伸長),再沿縱坐標軸進行伸縮( 縮短,
縮短,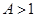 伸長).最后上下平移(上加下減);②先沿橫坐標軸進行伸縮(
伸長).最后上下平移(上加下減);②先沿橫坐標軸進行伸縮( 縮短,
縮短, 伸長),再左右平移(左加右減),再沿縱坐標軸進行伸縮(
伸長),再左右平移(左加右減),再沿縱坐標軸進行伸縮( 縮短,
縮短,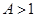 伸長).最后上下平移(上加下減).
伸長).最后上下平移(上加下減).
注意點:先伸縮后平移時,要注意平移的單位 的圖像由
的圖像由 向左或右平移
向左或右平移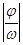 個單位.
個單位.
試題解析:(1)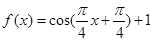 .
.
列表如下:
0 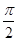
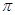
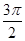

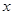
-1 1 3 5 7 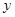
2 1 0 1 2 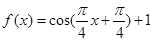 的簡圖如下:
的簡圖如下:
(2) 的圖像向左平移
的圖像向左平移 個單位得到
個單位得到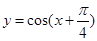 圖像的;縱坐標不變,橫坐標變為原來的
圖像的;縱坐標不變,橫坐標變為原來的 倍得到
倍得到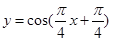 的圖像;向上平移1個單位得到
的圖像;向上平移1個單位得到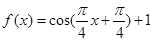 的圖像.
的圖像.
考點:三角恒等變換、三角函數的圖像變換.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
已知函數
(1)求函數 的最小正周期及單調遞減區間;
的最小正周期及單調遞減區間;
(2)若將函數的圖像向右平移 個單位,得到函數
個單位,得到函數 的圖像,求
的圖像,求 在區間
在區間 上的最大值和最小值,并求出相應的x的取值。
上的最大值和最小值,并求出相應的x的取值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=Acos(ωx+φ)(A>0,ω>0,- <φ<0)的圖象與y軸的交點為(0,1),它在y軸右側的第一個最高點和第一個最低點的坐標分別為(x0,2)和(x0+2π,-2).
<φ<0)的圖象與y軸的交點為(0,1),它在y軸右側的第一個最高點和第一個最低點的坐標分別為(x0,2)和(x0+2π,-2).
(1)求函數f(x)的解析式;
(2)若銳角θ滿足cosθ= ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com