(本小題滿分12分)
設(shè)命題

:方程
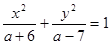
表示焦點在坐標(biāo)軸上的雙曲線,命題

:

。
(1)寫出命題

的否定;
(2)若“

或
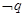
”為真命題,求實數(shù)
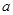
的取值范圍。
本試題主要是考查了命題的真值的判定以及復(fù)合命題的綜合運用。
(1)因為命題

:

。
可以利用全稱命題的否定得到結(jié)論。
(2)
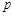
真,即方程
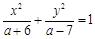
表示焦點在坐標(biāo)軸上的雙曲線,
則
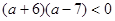
,
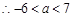
,而若
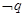
真,
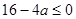

可知結(jié)論。
解:(1)
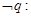
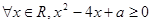
……………………4分
(2)若
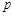
真,即方程
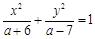
表示焦點在坐標(biāo)軸上的雙曲線,
則
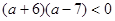
,
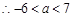
.
若
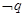
真,
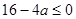

………………………………10分
因為“

或
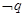
”為真命題,所以
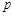
與
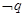
中至少有一個為真,
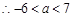
或
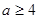
即
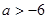
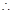
符合條件的實數(shù)
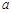
的取值范圍是
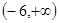
……………………12分
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知命題:
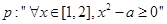
,命題
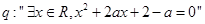
,若命題
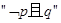
是真命題,則實數(shù)a的取值范圍是 ( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知命題p:?n∈N,2
n>1 000,則﹁p為( ).
| A.?n∈N,2n<1 000 | B.?n∈N,2n>1 000 |
| C.?n∈N,2n≤1 000 | D.?n∈N,2n≤1 000 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
下列四個命題中真命題是
P1:
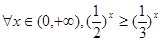
P2:
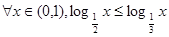
P3:
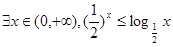
P4:

| A.P1,P3 | B.P1,P4 | C.P2,P3 | D.P2,P4 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知命題p:“
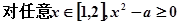
”,
命題q:“
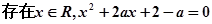
”若命題“p且q”是真命題,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知命題
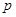
:“
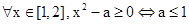
”,命題
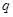
:“
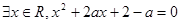
”.若命題“
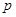
且
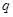
”是真命題,則實數(shù)
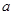
的取值范圍為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知
p:
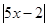
>3,
q:
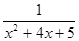
≥0,
(1)求滿足
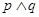
為真的
x的范圍:
(2)判斷
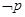
是
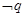
的什么條件?
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
設(shè)命題
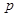
:若
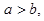
則
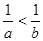
;
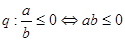
.給出下列四個復(fù)合命題:①
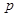
或

,②
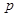
且

,③
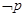
,④
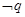
.其中真命題有( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
命題“
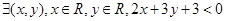
”的否定是( )
查看答案和解析>>

 :方程
:方程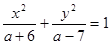 表示焦點在坐標(biāo)軸上的雙曲線,命題
表示焦點在坐標(biāo)軸上的雙曲線,命題 :
: 。
。 的否定;
的否定; 或
或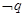 ”為真命題,求實數(shù)
”為真命題,求實數(shù)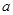 的取值范圍。
的取值范圍。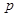 :若
:若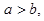 則
則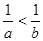 ;
;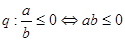 .給出下列四個復(fù)合命題:①
.給出下列四個復(fù)合命題:①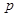 或
或 ,②
,②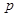 且
且 ,③
,③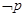 ,④
,④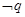 .其中真命題有( )
.其中真命題有( )