中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

雙曲線
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦點分別是F1，F(xiàn)2，過F1作傾斜角為30°的直線交雙曲線右支于M點，若MF2垂直于x軸，則雙曲線的離心率為（　　）
A．
6
B．
3
C．
2
D．
3
3

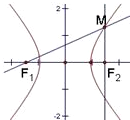
如圖在Rt△MF1F2中，∠MF1F2=30°，F(xiàn)1F2=2c
∴MF1=
2c
cos30°
=
4
3
3
c，MF2=2c•tan30°=
2
3
3
c
∴2a=MF1-MF2=
4
3
3
c-
2
3
3
c=
2
3
3
c
∴e=
c
a
=
3
，
故選B．
練習冊系列答案
相關(guān)習題

科目：高中數(shù)學(xué) 來源：不詳 題型：解答題

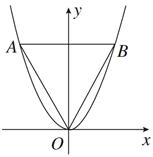
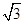
如圖，等邊三角形OAB的邊長為8，且其三個頂點均在拋物線E：x2＝2py(p>0)上．

(1)求拋物線E的方程；
(2)設(shè)動直線l與拋物線E相切于點P，與直線y＝－1相交于點Q，證明以PQ為直徑的圓恒過y軸上某定點．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：解答題

設(shè)雙曲線C：
x2
a2
-y2=1(a＞0)與直線l：x+y=1交于兩個不同的點A，B，求雙曲線C的離心率e的取值范圍．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：單選題

經(jīng)過雙曲線：
x2
4
-y2=1的右焦點的直線與雙曲線交于兩點A，B，若AB=4，則這樣的直線有幾條（　　）
A．1條B．2條C．3條D．4條

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：單選題

已如點M（1，0）及雙曲線
x2
3
-y2=1的右支上兩動點A，B，當∠AMB最大時，它的余弦值為（　　）
A．-
1
2
B．
1
2
C．-
1
3
D．
1
3

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：單選題

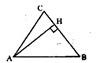
如圖，在△ABC中，tan
C
2
=
1
2
，
AH
•
BC
=0，則過點C，以A、H為兩焦點的雙曲線的離心率為（　　）
A．2B．3C．
2
D．
3

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：填空題

已知雙曲線C1：2x2-y2=8，雙曲線C2滿足：①C1與C2有相同的漸近線，②C2的焦距是C1的焦距的兩倍，③C2的焦點在y軸上，則C2的方程是______．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：單選題

已知雙曲線標準方程為：
x2
a2
-
y2
b2
=1(a＞0，b＞0)，一條漸近線方程為y=x，點P（2，1）在雙曲線的右支上，則a的值為（　　）
A．1B．2C．
3
D．3

查看答案和解析>>

科目：高中數(shù)學(xué) 來源：不詳 題型：解答題

已知A、B是雙曲線C：
x2
4
-
y2
3
=1的左、右頂點，P是坐標平面上異于A、B的一點，設(shè)直線PA、PB的斜率分別為k1，k2．
求證：k1k2=
3
4
是P點在雙曲線C上的充分必要條件．

查看答案和解析>>

同步練習冊答案