
思路分析:本題通過建立數學模型,把實際問題轉化為數學問題,然后利用函數求函數的最值.
解:S=|OP|2=x2+y2=x2+(x2-2x-1)2=x4-4x3+3x2+4x+1,
則S′=4x3-12x2+6x+4=2(x-2)(2x2-2x-1)=4(x-2)(x-![]() )(x-
)(x-![]() ).
).
令S′=0,則x1=![]() ,x2=
,x2=![]() ,x3=2.
,x3=2.
當x變化時,S′,S的變化情況如下表:
x | (-∞, |
| ( |
| ( | 2 | (2,+∞) |
S′ | - | 0 | + | 0 | - | 0 | + |
S | ?↘ | 極小值 | ?↗ | 極大值 | ↘? | 極小值 | ↗? |
∵S的定義域為(-∞,+∞),
∴所求的最小值是兩個極小值中較小的一個.
∵當x=![]() 時,S=(
時,S=(![]() )4-4(
)4-4(![]() )3+3(
)3+3(![]() )2+4(
)2+4(![]() )+1=
)+1=![]() ,
,
當x=2時,S=24-4×23+3×22+4×2+1=5,
∴S的最小值為![]() .
.


科目:高中數學 來源: 題型:
| OP |
| i |
| j |
| k |
| i |
| j |
| k |
| OP |
| i |
| j |
| k |
| OP |
| j |
| OP |
| i |
| 1 |
| x |
| 2 |
| y |
| 2 |
| OP |
| i |
| j |
| k |
| OQ |
| i |
| j |
| k |
| PQ |
| k |
| PQ |
| OP |
| OM |
| i |
| j |
| k |
| OQ |
| i |
| j |
| k |
| OR |
| i |
| j |
| k |
| x |
| a |
| y |
| b |
| z |
| c |
| OP |
| i |
| j |
| k |
| OM |
| i |
| j |
| k |
| ON |
| i |
| j |
| k |
| PM |
| j |
| PN |
| j |
| PM |
| PN |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年四川省成都市高三第二次診斷性檢測理科數學試卷(解析版) 題型:填空題
在空間直角坐標系O-xyz中,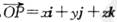 (其中i、j、k分別為X軸、y軸、z軸正方向上的單位向量).有下列命題:
(其中i、j、k分別為X軸、y軸、z軸正方向上的單位向量).有下列命題:
①若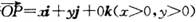 且
且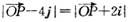 ,則
,則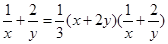
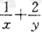 的最小值為
的最小值為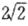 ;
;
②設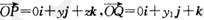 ,若向量
,若向量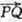 與k共線且
與k共線且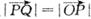 ,則動點P的軌跡是拋物線;
,則動點P的軌跡是拋物線;
③若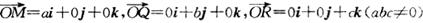 ,則平面MQR內的任意一點A (x,y,z)的坐標必然滿足關系式
,則平面MQR內的任意一點A (x,y,z)的坐標必然滿足關系式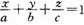 ;
;
④設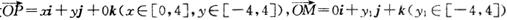 ,
,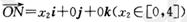 ,若向量
,若向量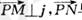 與j共線且
與j共線且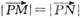 ,則動點P的軌跡是雙曲線的一部分.
其中你認為正確的所有命題的序號為. _______
,則動點P的軌跡是雙曲線的一部分.
其中你認為正確的所有命題的序號為. _______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com