
如圖,已知圓![]() 與
與![]() 軸負半軸的交點為
軸負半軸的交點為![]() . 由點
. 由點![]() 出發的射線
出發的射線![]() 的斜率為
的斜率為![]() . 射線
. 射線![]() 與圓
與圓![]() 相交于另一點
相交于另一點![]()

(1)當![]() 時,試用
時,試用![]() 表示點
表示點![]() 的坐標;
的坐標;
(2)當![]() 時,求證:“射線
時,求證:“射線![]() 的斜率
的斜率![]() 為有理數”是“點
為有理數”是“點![]() 為單位圓
為單位圓![]() 上的有理點”的充要條件;(說明:坐標平面上,橫、縱坐標都為有理數的點為有理點.我們知道,一個有理數可以表示為
上的有理點”的充要條件;(說明:坐標平面上,橫、縱坐標都為有理數的點為有理點.我們知道,一個有理數可以表示為![]() ,其中
,其中![]() 、
、![]() 均為整數且
均為整數且![]() 、
、![]() 互質)
互質)
(3)定義:實半軸長![]() 、虛半軸長
、虛半軸長![]() 和半焦距
和半焦距![]() 都是正整數的雙曲線為“整勾股雙曲線”.
都是正整數的雙曲線為“整勾股雙曲線”.
當![]() 為有理數且
為有理數且![]() 時,試證明:一定能構造偶數個“整勾股雙曲線”(規定:實軸長和虛軸長都對應相等的雙曲線為同一個雙曲線),它的實半軸長、虛半軸長和半焦距的長恰可由點
時,試證明:一定能構造偶數個“整勾股雙曲線”(規定:實軸長和虛軸長都對應相等的雙曲線為同一個雙曲線),它的實半軸長、虛半軸長和半焦距的長恰可由點![]() 的橫坐標、縱坐標和半徑
的橫坐標、縱坐標和半徑![]() 的數值構成. 說明你的理由并請嘗試給出構造方法.
的數值構成. 說明你的理由并請嘗試給出構造方法.
(1)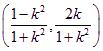 (2)證明略 (3)略
(2)證明略 (3)略
(1)解:設點![]() 的坐標為
的坐標為![]() . 由題意,點
. 由題意,點![]() 的坐標為
的坐標為![]() ,
,
于是可設射線![]() 的方程為
的方程為![]() ,
,
代入圓![]() 的方程可得:
的方程可得:![]()
![]() …①
…①
方程①中,一個解必為![]() ,則由根與系數關系可知
,則由根與系數關系可知
點![]() 的橫坐標為
的橫坐標為![]() ;代入直線方程可得
;代入直線方程可得![]() .所以,點
.所以,點![]() 的坐標即為
的坐標即為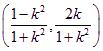 .
.
(2)充分性:設射線![]() 的斜率
的斜率![]() (其中
(其中![]() 、
、![]() 均為整數且
均為整數且![]() 、
、![]() 互質)
互質)
則由(1)可知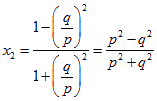 ,
,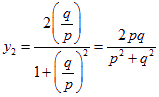 .
.
因為![]() 、
、![]() 均為整數,所以
均為整數,所以![]() 、
、![]() 必為一個有理數,從而
必為一個有理數,從而![]() 點必為一個有理點.
點必為一個有理點.
必要性:若![]() 點為有理點,則可設
點為有理點,則可設![]() ,
,![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均為整數且
均為整數且![]() 和
和![]() 互質、
互質、![]() 和
和![]() 互質)
互質)
于是,![]() ,因為
,因為![]() 、
、![]() 、
、![]() 、
、![]() 均為整數,所以
均為整數,所以![]() 必為一個有理數.
必為一個有理數.
(3)證:設![]() 點的坐標為
點的坐標為![]() .當
.當![]() 時,
時,![]() 點必定落在第一象限的四分之一圓周上,即
點必定落在第一象限的四分之一圓周上,即![]() ,
,![]() .
.
而由![]() ,所以
,所以![]() 的橫坐標
的橫坐標![]() 、縱坐標
、縱坐標![]() 以及圓的半徑
以及圓的半徑![]() 必能構成某個雙曲線的一組實半軸長、虛半軸長和半焦距的數據. 由(2)結論可知,
必能構成某個雙曲線的一組實半軸長、虛半軸長和半焦距的數據. 由(2)結論可知,
此時點![]() 的坐標應為
的坐標應為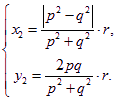 其中
其中![]() 、
、![]() 此時均為正整數且
此時均為正整數且![]() 、
、![]() 互質.
互質.
于是,只要構造圓半徑![]() (其中
(其中![]() 為正整數)時,則會有
為正整數)時,則會有
![]() ,
,![]() ,它們都為正整數,且滿足
,它們都為正整數,且滿足![]() .
.
因此,對于斜率為![]() (其中
(其中![]() 、
、![]() 均為整數,
均為整數,![]() 且
且![]() 、
、![]() 互質)的斜線
互質)的斜線![]() ,只需確定圓的半徑滿足
,只需確定圓的半徑滿足![]() (其中
(其中![]() 為正整數),則必定能構造“整勾股雙曲線”滿足題意.
為正整數),則必定能構造“整勾股雙曲線”滿足題意.
特別地,因為當![]() 時,點
時,點![]() 坐標必為
坐標必為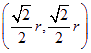 ,而此時射線
,而此時射線![]() 的斜率為
的斜率為![]() ,不是有理數.所以,構造出的雙曲線一定不是等軸雙曲線,
,不是有理數.所以,構造出的雙曲線一定不是等軸雙曲線,
即由![]() ,可構造的“整勾股雙曲線”的實半軸長、虛半軸長和半焦距長可由
,可構造的“整勾股雙曲線”的實半軸長、虛半軸長和半焦距長可由 和
和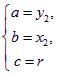 構成,且個數一定為偶數個.
構成,且個數一定為偶數個.


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:
 (2006•朝陽區二模)如圖,已知圓C:(x-1)2+y2=r2(r>1),設M為圓C與x軸負半軸的交點,過M作圓C的弦MN,并使它的中點P恰好落在y軸上.
(2006•朝陽區二模)如圖,已知圓C:(x-1)2+y2=r2(r>1),設M為圓C與x軸負半軸的交點,過M作圓C的弦MN,并使它的中點P恰好落在y軸上.| CE |
| CF |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2009•普陀區一模)如圖,已知圓C:x2+y2=r2與x軸負半軸的交點為A.由點A出發的射線l的斜率為k,且k為有理數.射線l與圓C相交于另一點B.
(2009•普陀區一模)如圖,已知圓C:x2+y2=r2與x軸負半軸的交點為A.由點A出發的射線l的斜率為k,且k為有理數.射線l與圓C相交于另一點B.| q | p |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•濰坊一模)如圖,已知圓C與y軸相切于點T(0,2),與x軸正半軸相交于兩點M,N(點M必在點N的右側),且|MN|=3橢圓D:
(2013•濰坊一模)如圖,已知圓C與y軸相切于點T(0,2),與x軸正半軸相交于兩點M,N(點M必在點N的右側),且|MN|=3橢圓D:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,已知圓C:![]() ,設M為圓C與x軸負半軸的交點,過M作圓C的弦MN,并使它的中點P恰好落在y軸上.
,設M為圓C與x軸負半軸的交點,過M作圓C的弦MN,并使它的中點P恰好落在y軸上.
(Ⅰ)當r=2時, 求滿足條件的P點的坐標;
(Ⅱ)當r∈(1,+∞)時,求點N的軌跡G的方程;
(Ⅲ)過點P(0,2)的直線l與(Ⅱ)中軌跡G相交于兩個不同的點E、F,若![]() ,求直線
,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com