
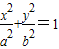 (a>b>0)的左、右焦點分別為F1(-1,0)、F2(1,0),離心率為
(a>b>0)的左、右焦點分別為F1(-1,0)、F2(1,0),離心率為 .
. (O為坐標原點),求△AOB的面積;
(O為坐標原點),求△AOB的面積;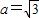 ,求出b 值,最后寫出橢圓C的方程即可;
,求出b 值,最后寫出橢圓C的方程即可; ”結合向量的數量積,代入三角形面積公式求得答案.
”結合向量的數量積,代入三角形面積公式求得答案. ,∴
,∴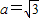
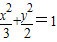
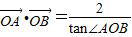 ,∴
,∴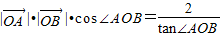 ,
, ,∴
,∴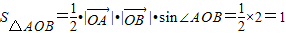 .
. 消去y得(3k2+2)x2-6k2x+3k2-6=0
消去y得(3k2+2)x2-6k2x+3k2-6=0
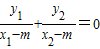 對一切k恒成立
對一切k恒成立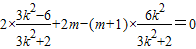 對一切k恒成立,
對一切k恒成立,

 智慧小復習系列答案
智慧小復習系列答案科目:高中數學 來源: 題型:
| 3 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 2 |
| 1 |
| 2 |
| OA |
| OB |
| 2OM |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
已知橢![]() 圓C:
圓C: ![]() +
+![]() =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e=![]() ,且橢圓經過點N(2,-3).
,且橢圓經過點N(2,-3).
(1)求橢圓C的方程;
(2)求橢圓以M(-1,2)為中點的弦所在直線的方程.
查看答案和解析>>
科目:高中數學 來源:2013屆福建省南安市高二上學期期末文科數學試卷 題型:解答題
已知橢圓C過點A(1, ),兩個焦點為(-1,0)(1,0)。
),兩個焦點為(-1,0)(1,0)。
求橢圓C的方程;
E,F是橢圓C上的兩個動點,如果直線AE的斜率與AF的斜率互為相反數,證明直線EF的斜率為定值,并求出這個定值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com