
已知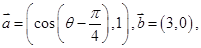 其中
其中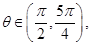 若
若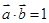 .
.
(1)求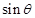 的值;
的值;
(2)求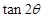 的值.
的值.
 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:解答題
設平面向量a=(cosx,sinx),b=(cosx+2 ,sinx),x∈R.
,sinx),x∈R.
(1)若x∈(0, ),證明:a和b不平行;
),證明:a和b不平行;
(2)若c=(0,1),求函數f(x)=a·(b-2c)的最大值,并求出相應的x值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知a=(5 cos x,cos x),b=(sin x,2cos x),設函數f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),設函數f(x)=a·b+|b|2+ .
.
(1)當∈ 時,求函數f(x)的值域;
時,求函數f(x)的值域;
(2)當x∈ 時,若f(x)=8,求函數f
時,若f(x)=8,求函數f 的值;
的值;
(3)將函數y=f(x)的圖象向右平移 個單位后,再將得到的圖象上各點的縱坐標向下平移5個單位,得到函數y=g(x)的圖象,求函數g(x)的表達式并判斷奇偶性.
個單位后,再將得到的圖象上各點的縱坐標向下平移5個單位,得到函數y=g(x)的圖象,求函數g(x)的表達式并判斷奇偶性.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=sin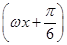 +
+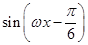 -2cos2
-2cos2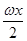 ,x∈R(其中ω>0).
,x∈R(其中ω>0).
(1)求函數f(x)的值域;
(2)若函數y=f(x)的圖象與直線y=-1的兩個相鄰交點間的距離為 ,求函數y=f(x)的單調增區間.
,求函數y=f(x)的單調增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=sin sin(
sin( +
+ ).
).
(1)求函數f(x)在[-π,0]上的單調區間.
(2)已知角α滿足α∈(0, ),2f(2α)+4f(
),2f(2α)+4f( -2α)=1,求f(α)的值.
-2α)=1,求f(α)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知點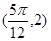 在函數
在函數 的圖象上,直線
的圖象上,直線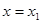 、
、 是
是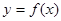 圖象的任意兩條對稱軸,且
圖象的任意兩條對稱軸,且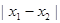 的最小值為
的最小值為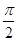 .
.
(1)求函數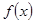 的單遞增區間和其圖象的對稱中心坐標;
的單遞增區間和其圖象的對稱中心坐標;
(2)設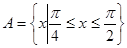 ,
,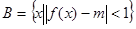 ,若
,若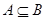 ,求實數
,求實數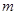 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知m=(2cos x+2 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)將y表示為x的函數f(x),并求f(x)的單調增區間;
(2)已知a,b,c分別為△ABC的三個內角A,B,C對應的邊長,若f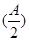 =3,且a=2,b+c=4,求△ABC的面積.
=3,且a=2,b+c=4,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com