兩個人射擊，甲射擊一次中靶概率是
，乙射擊一次中靶概率是
，
（Ⅰ）兩人各射擊1次，兩人總共中靶至少1次就算完成目標，則完成目標概率是多少？
（Ⅱ）兩人各射擊2次，兩人總共中靶至少3次就算完成目標，則完成目標的概率是多少？
（Ⅲ）兩人各射擊5次，兩人總共中靶至少1次的概率是否超過99％？
科目：高中數學 來源： 題型：解答題
為了防止受污染的產品影響我國民眾的身體健康，要求產品在進入市場前必須進行兩輪檢測，只有兩輪都合格才能進行銷售，否則不能銷售.已知某產品第一輪檢測不合格的概率為
，第二輪檢測不合格的概率為
，兩輪檢測是否合格相互沒有影響.
（Ⅰ）求該產品不能銷售的概率；
（Ⅱ）如果產品可以銷售，則每件產品可獲利40元；如果產品不能銷售，則每件產品虧損80元（即獲利-80元）.已知一箱中有產品4件，記一箱產品獲利X元，求X的分布列，并求出均值E(X).
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在某校組織的一次籃球定點投籃測試中，規定每人最多投
次，每次投籃的結果相互獨立.在
處每投進一球得分，在
處每投進一球得
分，否則得
分. 將學生得分逐次累加并用
表示，如果的值不低于分就認為通過測試，立即停止投籃，否則繼續投籃，直到投完三次為止.投籃的方案有以下兩種：方案1：先在處投一球，以后都在處投；方案2：都在處投籃.甲同學在處投籃的命中率為
，在處投籃的命中率為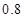
.
（Ⅰ）甲同學選擇方案1.
求甲同學測試結束后所得總分等于4的概率；
求甲同學測試結束后所得總分的分布列和數學期望
；
（Ⅱ）你認為甲同學選擇哪種方案通過測試的可能性更大？說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
一個盒子裝有6張卡片，上面分別寫著如下6個定義域為R的函數：
，
，
，
，
，
.
(1)現從盒子中任取兩張卡片，將卡片上的函數相加得到一個新函數，求所得函數是奇函數的概率；
(2)現從盒子中逐一抽取卡片，且每次取出后均不放回，若取到一張記有偶函數的卡片則停止抽取，否則繼續進行，求抽取次數ξ的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某廣場上有4盞裝飾燈，晚上每盞燈都隨機地閃爍紅燈或綠燈，每盞燈出現紅燈的概率都是
，出現綠燈的概率都是
．記這4盞燈中出現紅燈的數量為
，當這排裝飾燈閃爍一次時：
（1）求
時的概率；（2）求的數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某學生在上學路上要經過4個路口，假設在各路口是否遇到紅燈是相互獨立的，遇到紅燈的概率都是
，遇到紅燈時停留的時間都是2 分鐘. 設這名學生在路上遇到紅燈的個數為變量
、停留的總時間為變量
，
（1）求這名學生在上學路上到第三個路口時首次遇到紅燈的概率；
（2）這名學生在上學路上遇到紅燈的個數至多是2個的概率.
（3）求的標準差
．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在平面
內，不等式
確定的平面區域為
，不等式組
確定的平面區域為
.
（1）定義橫、縱坐標為整數的點為“整點”. 在區域中任取3個“整點”，求這些“整點”中恰好有2個“整點”落在區域中的概率；
（2）在區域中每次任取一個點，連續取3次，得到3個點，記這3個點落在區域中的個數為
，求的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某中學校本課程共開設了A，B，C，D共4門選修課，每個學生必須且只能選修1門選修課，現有該校的甲、乙、丙3名學生：
（1）求這3名學生選修課所有選法的總數；
（2）求恰有2門選修課沒有被這3名學生選擇的概率；
（3）求A選修課被這3名學生選擇的人數的數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）
根據公安部最新修訂的《機動車駕駛證申領和使用規定》：每位駕駛證申領者必須通過《科目一》（理論科目）、《綜合科》（駕駛技能加科目一的部分理論）的考試.已知李先生已通過《科目一》的考試，且《科目一》的成績不受《綜合科》的影響，《綜合科》三年內有5次預約考試的機會，一旦某次考試通過，便可領取駕駛證，不再參加以后的考試，否則就一直考到第5次為止.設李先生《綜合科》每次參加考試通過的概率依次為0.5，0.6，0.7，0.8，0.9．
（1）求在三年內李先生參加駕駛證考試次數
的分布列和數學期望；
（2）求李先生在三年內領到駕駛證的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
（Ⅱ）
（Ⅲ）超過
； 甲中靶乙不中
； 
。 ∴概率是
. 4分
；
，
． 10分
，超過. 14分
