中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知函數f(x)的圖像與函數h(x)＝x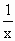＋＋2的圖像關于點A(0，1)對稱．

(1)求f(x)的解析式；

(2)(文)若g(x)＝f(x)·x＋ax，且g(x)在區間(0，2]上為減函數，求實數a的取值范圍；

(理)若g(x)＝f(x)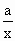＋，且g(x)在區間(0，2]上為減函數，求實數a的取值范圍．

答案：
解析：

 　　解：(1)設f(x)圖像上任一點坐標為(x，y)，點(x，y)關于點A(0，1)的對稱點(－x，2－y)在h(x)圖像上

　　解：(1)設f(x)圖像上任一點坐標為(x，y)，點(x，y)關于點A(0，1)的對稱點(－x，2－y)在h(x)圖像上

　　∴2－y＝－x＋＋2，∴y＝x＋，即f(x)＝x＋

　　(2)文：g(x)＝(x＋)·x＋ax，即g(x)＝x2＋ax＋1

　　g(x)在(0，2]上遞減－≥2，∴a≤－4

　　理：g(x)＝x＋，∵(x)＝1－

　　g(x)在(0，2]上遞減，∴1－≤0在x∈(0，2]時恒成立．

　　即a≥x2－1在x∈(0，2]時恒成立．

　　∵x∈(0，2]時，(x2－1)max＝3　　∴a≥3


練習冊系列答案
相關習題

科目：高中數學 來源：成功之路·突破重點線·數學（學生用書） 題型：044

已知函數f(x)＝2acos2x＋bsinxcosx，且f(0)＝2，f()＝，

(1)求使f(x)＞2的x的集合；

(2)若α－β≠kπ(k∈Z)，且f(α)＝f(β)，求tan(α＋β)的值．

查看答案和解析>>

科目：高中數學 來源：成功之路·突破重點線·數學（學生用書） 題型：044

已知函數f(x)＝x3＋(m－4)x2－3mx＋(n－6)(x∈R)的圖象關于原點對稱，m，n為實常數．

(1)求m，n的值；

(2)試用單調性的定義證明f(x)在區間[－2，2]上是單調函數

(3)當x∈[－2，2]時，不等式f(x)≥(n－logma)logma恒成立，求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源：廣東省開平市長師中學2007年高考數學文科第一輪復習階段性考試卷 題型：044

解答題

已知函數在同一周期內有最高點和最低點，求此函數的解析式．

查看答案和解析>>

科目：高中數學 來源：龍門中學、新豐一中、連平中學三校聯考試題、高三數學(理) 題型：044

解答題

已知函數恒過點．

(1)

求的值；

(2)

求函數的最小正周期及單調遞減區間．

查看答案和解析>>

科目：高中數學 來源：2007龍門中學、新豐一中、連平中學三校聯考試題、高三數學(文) 題型：044

解答題

已知函數恒過點．

(1)

求的值；

(2)

求函數的最小正周期及單調遞減區間．

查看答案和解析>>

同步練習冊答案