
如下圖:設
a、b是異面直線,A∈a,B∈b,AB⊥a,AB⊥b,過AB的中點O作平面α與a、b分別平行,M、N分別是a、b上任意兩點,MN與α交于點P,求證:
P是MN的中點.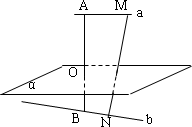
 計算高手系列答案
計算高手系列答案科目:高中數學 來源: 題型:044
(2005
山東,22)如下圖,已知動圓過定點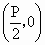 ,且與直線
,且與直線 相切,其中p>0,
相切,其中p>0,
(1)
求動圓圓心的軌跡C的方程;(2)
設A、B是軌跡C上異于原點O的兩個不同點,直線OA和OB的傾斜角分別為α和β,當α、β變化且α+β為定值θ(0<θ<π)時,證明:直線AB恒過定點,并求出該定點的坐標.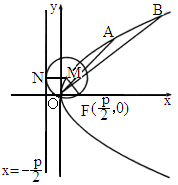
查看答案和解析>>
科目:高中數學 來源: 題型:
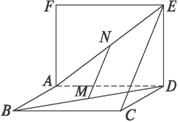
①AD⊥MN ② MN∥面CDE ③MN∥CE ④MN、CE是異面直線
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com