
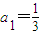 ,且對于任意的正整數m,n都有
,且對于任意的正整數m,n都有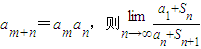 =( )
=( )


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源:2011年四川省南充市高中高三最后一次月考數學試卷(文科)(解析版) 題型:解答題
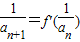 ,且a1=4,求數列an的通項公式;
,且a1=4,求數列an的通項公式;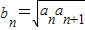 ,數列bn的前n項和Tn,求證:
,數列bn的前n項和Tn,求證: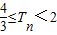 .
.查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省部分重點中學聯考高三(上)期中數學試卷(理科)(解析版) 題型:選擇題
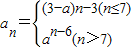 且{an}是遞增數列,則實數a的范圍是( )
且{an}是遞增數列,則實數a的范圍是( )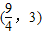
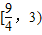
查看答案和解析>>
科目:高中數學 來源:2013年廣東省深圳中學高考數學二模試卷(理科)(解析版) 題型:解答題
 ,且a1=4,求數列{an} 的通項公式;
,且a1=4,求數列{an} 的通項公式;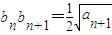 ,當n≥3,n∈N*時,求證:①
,當n≥3,n∈N*時,求證:①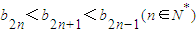 ;②
;②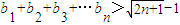 .
.查看答案和解析>>
科目:高中數學 來源:2011年湖北省武漢市華師一附中高三5月模擬數學試卷(文科)(解析版) 題型:解答題
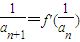 ,且a1=4,求數列an的通項公式;
,且a1=4,求數列an的通項公式; ,數列bn的前n項和Tn,求證:
,數列bn的前n項和Tn,求證: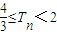 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com