Question

定義在上的函數，如果對任意，恒有（，）成立，則稱為階縮放函數.
（1）已知函數為二階縮放函數，且當時，，求的值；
（2）已知函數為二階縮放函數，且當時，，求證：函數在上無零點；
（3）已知函數為階縮放函數，且當時，的取值范圍是，求在（）上的取值范圍.

Answer 1

（1）1；（2）詳見解析；（3）.

解析試題分析：(1)本小題首先利用函數為二階縮放函數，所以，于是由得，，由題中條件得；
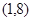(2)本小題首先對時，，得到，方程或，與均不屬于（），所以當時，方程無實數解，所以函數在上無零點；
(3)本小題針對，時，有，依題意可得，然后通過分析可得取值范圍為.
試題解析：（1）由得，      2分
由題中條件得        4分
（2）當時，，依題意可得：
。  6分
方程或，
與均不屬于（）  8分
當（）時，方程無實數解。
注意到，所以函數在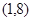上無零點。 10分
（3）當，時，有，依題意可得：

當時，的取值范圍是 12分
所以當，時，的取值范圍是。 14分
由于 16分
所以函數在（）上的取值范圍是：
。 18分
考點：1.新定義；2.函數的單調性.