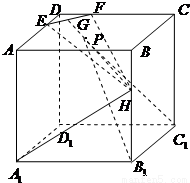
分析:(1)由題意建立坐標系,求出平面EFH的法向量,利用對應向量的數量積求出線面角的余弦值,再求其正弦值;
(2)由題意先求出P點的坐標,再求向量
的長度的平方,轉化為關于λ的一個一元二次函數,當取在對稱軸出有最小值.
解答:解:由題意,以D
1為坐標原點,A
1D
1,D
1C
1,DD
1為x,y,z軸建立直角坐標系
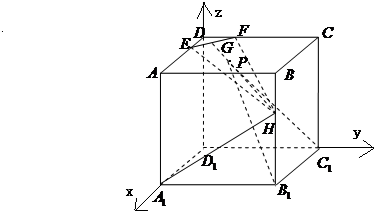
,
可得E(2,0,6),F(0,2,6),H(6,6,4),A
1(6,0,0).
(1)設平面EFH的法向量
=(1,x,y),∵
=(-2,2,0),
=(4,6,-2)
∴
,求得
=(1,1,5);
∵
=(0,6,4),∴cos<
,
>=
=
=
;
設A
1H 與平面EF所成角θ,則cosθ=
=
.(5分)
(2)由題意知,G(1,1,6),C
1(0,6,0),
=(5,5,-2),
∵
=λ,∴設
=λ
=(5λ,5λ,-2λ),解得P(5λ+1,5λ+1,-2λ+6),
∴
=(5λ+1,5λ-5,-2λ+6),
∴
2=(5λ+1)
2+(5λ-5)
2+(2λ-6)
2=54λ
2-64λ+58,
當λ=
時,C
1P的長度取得最小值.(10分)
點評:本題用向量法求線面角的問題及求線段的最小值,只要用了向量的數量積和向量的長度;在求長度時轉化到了二次函數求最小值,考查了轉化思想和運算能力.

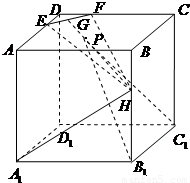
 已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點.
已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點. ,
,

 已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點.
已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點.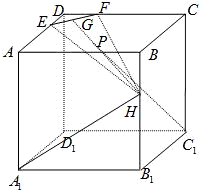 已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點.
已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點.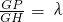 ,試確定λ的值,使得C1P的長度最短.
,試確定λ的值,使得C1P的長度最短.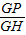 =λ,試確定λ的值,使得二面角P-C1B1-A1的余弦值為
=λ,試確定λ的值,使得二面角P-C1B1-A1的余弦值為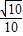 .
.
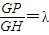 ,試確定λ的值,使得C1P的長度最短.
,試確定λ的值,使得C1P的長度最短.