
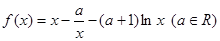 .
.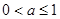 時,求函數(shù)
時,求函數(shù)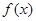 的單調區(qū)間;
的單調區(qū)間;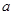 ,使
,使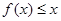 恒成立,若存在,求出實數(shù)
恒成立,若存在,求出實數(shù)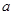 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.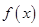 的單調增區(qū)間為
的單調增區(qū)間為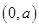 和
和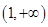 ,單調減區(qū)間為
,單調減區(qū)間為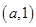
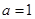 時,
時, 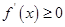 ,
,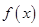 的單調增區(qū)間為
的單調增區(qū)間為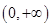
 時,使
時,使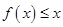 恒成立.
恒成立. 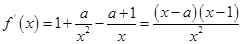 ,根據(jù)定義域
,根據(jù)定義域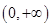 ,然后討論對a進行討論確定單調區(qū)間。
,然后討論對a進行討論確定單調區(qū)間。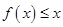 恒成立可轉化為
恒成立可轉化為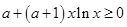 恒成立,
恒成立,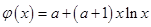 ,則只需
,則只需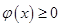 在
在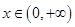 恒成立即可.然后再利用導數(shù)研究其最值,問題得解。
恒成立即可.然后再利用導數(shù)研究其最值,問題得解。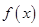 的定義域為
的定義域為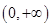 ,
,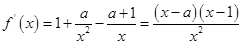 …………………………2分
…………………………2分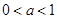 時,由
時,由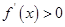 得,
得,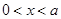 或
或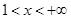 ,由
,由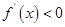 得,
得,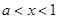
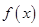 的單調增區(qū)間為
的單調增區(qū)間為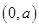 和
和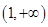 ,單調減區(qū)間為
,單調減區(qū)間為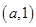 …………4分
…………4分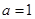 時,
時, 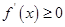 ,
,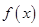 的單調增區(qū)間為
的單調增區(qū)間為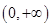 …………………………5分
…………………………5分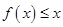 恒成立可轉化為
恒成立可轉化為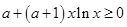 恒成立,
恒成立,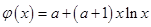 ,則只需
,則只需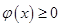 在
在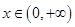 恒成立即可,………6分
恒成立即可,………6分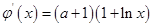
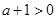 時,在
時,在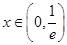 時,
時,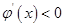 ,在
,在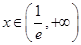 時,
時,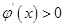
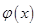 的最小值為
的最小值為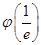 ,由
,由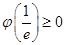 得
得 ,
, 時
時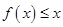 恒成立, ……………………………………9分
恒成立, ……………………………………9分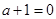 時,
時,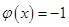 ,
,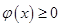 在
在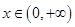 不能恒成立,……………11分
不能恒成立,……………11分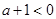 時,取
時,取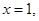 有
有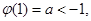
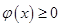 在
在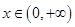 不能恒成立,…13分
不能恒成立,…13分 時,使
時,使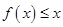 恒成立. ………………………14分
恒成立. ………………………14分

國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com