
已知M (-3,0)﹑N (3,0),P為坐標平面上的動點,且直線PM與直線PN的斜率之積為常數(shù)m (m
 ,m
,m 0),點P的軌跡加上M、N兩點構成曲線C.
0),點P的軌跡加上M、N兩點構成曲線C.
求曲線C的方程并討論曲線C的形狀;
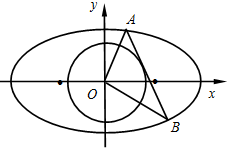
(2) 若 ,曲線C過點Q (2,0) 斜率為
,曲線C過點Q (2,0) 斜率為 的直線
的直線 與曲線C交于不同的兩點A﹑B,AB中點為R,直線OR (O為坐標原點)的斜率為
與曲線C交于不同的兩點A﹑B,AB中點為R,直線OR (O為坐標原點)的斜率為 ,求證
,求證  為定值;
為定值;
(3) 在(2)的條件下,設 ,且
,且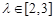 ,求
,求 在y軸上的截距的變化范圍.
在y軸上的截距的變化范圍.
(1)
若m=-1,則方程為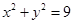 ,軌跡為圓;
,軌跡為圓;
若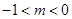 ,方程為
,方程為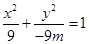 ,軌跡為橢圓;
,軌跡為橢圓;
若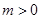 ,方程為
,方程為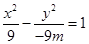 ,軌跡為雙曲線
,軌跡為雙曲線
(2)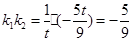
(3)
【解析】
試題分析:解:(1)由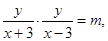 得點P的軌跡方程為:
得點P的軌跡方程為: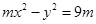 .
.
若m=-1,則方程為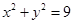 ,軌跡為圓;
,軌跡為圓;
若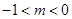 ,方程為
,方程為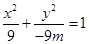 ,軌跡為橢圓;
,軌跡為橢圓;
若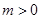 ,方程為
,方程為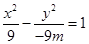 ,軌跡為雙曲線。
4分
,軌跡為雙曲線。
4分
(2)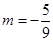 時,曲線C方程為
時,曲線C方程為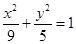 ,
,
設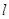 的方程為:
的方程為: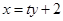 ,與曲線C方程聯(lián)立得:
,與曲線C方程聯(lián)立得: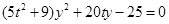 ,
,
設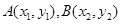 ,則
,則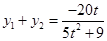 ①,
①,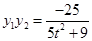 ②,
②,
可得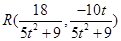 , ∴
, ∴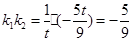 為定值。
7分
為定值。
7分
注:①可用點差法證明;②直接用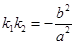 得出結果的,本小題只給1分.
得出結果的,本小題只給1分.
(3)由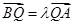 得
得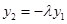 代入①②得:
代入①②得: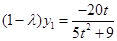 ③,
③,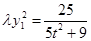 ④,
④,
③式平方除以④式得: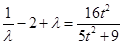 ,
,
∵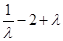 在
在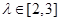 上單調(diào)遞增,∴
上單調(diào)遞增,∴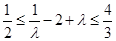 ,∴
,∴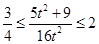 ,可得
,可得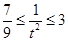
又∵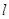 在y軸上的截距
在y軸上的截距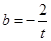 ,∴
,∴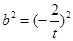 =
=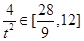 ,
,
∴ ,此即為
,此即為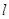 在y軸上的截距的變化范圍。 10分
在y軸上的截距的變化范圍。 10分
考點:直線與橢圓的位置關系
點評:解決的關鍵是根據(jù)直線與橢圓聯(lián)立方程組來結合韋達定理來求解,屬于中檔題。


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數(shù)學 來源: 題型:
| 3 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| OF1 |
| OF2 |
| MF1 |
| MF2 |
| OP |
| OQ |
| ||||
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 已知M(-
已知M(-| 3 |
| 3 |
| 6 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com