
(2)已知af(x)+bf(![]() )=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
)=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
(3)f(x)是R上的奇函數,且x∈(-∞,0)時,f(x)=x2+2x,求f(x);
(4)某工廠生產一種機器的固定成本為5 000元,且每生產100部,需要增加投入2 500元,對銷售市場進行調查后得知,市場對此產品的需求量為每年500部,已知銷售收入的函數為H(x)=500x-![]() x2,其中x是產品售出的數量,且0≤x≤500.若x為年產量,y表示利潤,求y=f(x)的解析式.
x2,其中x是產品售出的數量,且0≤x≤500.若x為年產量,y表示利潤,求y=f(x)的解析式.
思路分析:已知函數的模型(如一次函數、反比例函數、二次函數等)一般設出函數解析式,由題設確定系數,即待定系數法,如(1);求抽象函數解析式,可以以變量換變量,然后解方程組求解析式,如(2),也可根據函數奇偶性確定解析式,如(3);實際應用問題的函數解析式則要符合實際意義.
解:(1)設g(x)=ax+b(a>0),a2x2+2abx+b2=4x2-20x+25(a>0).解得
∴g(x)=2x-5.
(2)由題設af(x)+bf(![]() )=cx,用x代換上式中的
)=cx,用x代換上式中的![]() ,則af(
,則af(![]() )+bf(x)=
)+bf(x)=![]() ,列方程組
,列方程組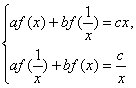 解得f(x)=
解得f(x)=![]() (ax-
(ax-![]() ).
).
(3)由于f(x)的定義域是R,且f(x)是奇函數,可得f(0)=0.
當x>0時,-x<0,則f(-x)=(-x)2-2x=x2-2x.
∴-f(x)=x2-2x,即f(x)=-x2+2x(x>0).
∴f(x)=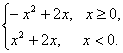
(4)由題意知,當0≤x≤500時,產品全部售出;當x>500時,只能售出500部,故利潤函數
y=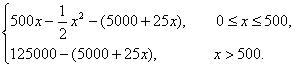
=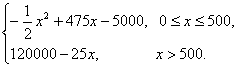


 全能練考卷系列答案
全能練考卷系列答案科目:高中數學 來源: 題型:
| 1+x2 |
| b(1+x2) |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(2)已知函數f(x)滿足f(x+y)+f(x-y)=![]() )=0,求f(π)及f(2π).
)=0,求f(π)及f(2π).
查看答案和解析>>
科目:高中數學 來源: 題型:閱讀理解
仔細閱讀下面問題的解法:
設A=[0, 1],若不等式21-x-a>0在A上有解,求實數a的取值范圍。
解:由已知可得 a < 21-x
令f(x)= 21-x ,∵不等式a <21-x在A上有解,
∴a <f(x)在A上的最大值.
又f(x)在[0,1]上單調遞減,f(x)max =f(0)=2. ∴實數a的取值范圍為a<2.
研究學習以上問題的解法,請解決下面的問題:
(1)已知函數f(x)=x2+2x+3(-2≤x≤-1),求f(x)的反函數及反函數的定義域A;
(2)對于(1)中的A,設g(x)=![]() ,x∈A,試判斷g(x)的單調性(寫明理由,不必證明);
,x∈A,試判斷g(x)的單調性(寫明理由,不必證明);
(3)若B ={x|![]() >2x+a–5},且對于(1)中的A,A∩B≠F,求實數a的取值范圍。
>2x+a–5},且對于(1)中的A,A∩B≠F,求實數a的取值范圍。
查看答案和解析>>
科目:高中數學 來源:新課標高三數學函數的圖象奇偶性、周期性專項訓練(河北) 題型:解答題
若函數f(x)對定義域中任意x均滿足f(x)+f(2a-x)=2b,則稱函數y=f(x)的圖象關于點(a,b)對稱.
(1)已知函數f(x)=的圖象關于點(0,1)對稱,求實數m的值;
(2)已知函數g(x)在(-∞,0)∪(0,+∞)上的圖象關于點(0,1)對稱,且當x∈(0,+∞)時,g(x)=x2+ax+1,求函數g(x)在(-∞,0)上的解析式;
(3)在(1)(2)的條件下,當t>0時,若對任意實數x∈(-∞,0),恒有g(x)<f(t)成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com