Question

已知x、y為正實數,且滿足關系式x²-2x+4y²=0,求x·y的最大值.

Answer 1

分析:題中有兩個變量x和y,首先應選擇一下因變量,將x、y表示為某一個變量(x或y或其他變量)的函數關系,實現問題的轉化.同時根據題設條件確定變量的取值范圍,再利用導數(或均值不等式等)求函數的最大值.

解法一:4y²=2x-x²,∵y＞0,∴y=.

∴x·y=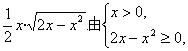解得0＜x≤2.

設f(x)=xy=(0＜x≤2).

當0＜x＜2時,f′(x)=

令f′(x)=0，得x=或x=0（舍去）.

∴.又f(2)=0,∴函數f(x)的最大值為,即x·y的最大值為.

解法二:由x²-2x+4y²=0,得(x-1)²+4y²=1(x＞0,y＞0).

設x-1=cosα,y=sinα(0＜α＜π),

∴x·y=sinα(1+cosα).

設f(α)= sinα(1+cosα),

則f′(α)= ［-sin²α+(1+cosα)·cosα］

=(2cos²α+cosα-1)=(cosα+1)(cosα-).

令f′(α)=0,得cosα=-1或cosα=.

∵0＜α＜π,∴α=,此時x=,y=.

∴f(α)_max=

即當x=,y=時,(x·y)_max=.

綠色通道:明確解決問題的策略、指向和思考方法需要抓住問題的本質,領悟真諦,巧施轉化.在實現轉化的過程中,關鍵是要注意變量的取值范圍必須滿足題設條件以免解題時陷于困境,功虧一簣.