

 的值;
的值; 成立的x的取值集合.
成立的x的取值集合.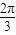 代入f(x)解析式,利用兩角和與差的余弦函數公式及特殊角的三角函數值化簡即可得到結果;
代入f(x)解析式,利用兩角和與差的余弦函數公式及特殊角的三角函數值化簡即可得到結果;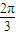 )=cos
)=cos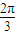 cos(
cos(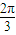 -
-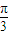 )=cos
)=cos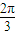 cos
cos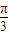 =-cos2
=-cos2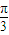 =-
=- ;
;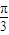 )=cosx(
)=cosx( cosx+
cosx+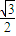 sinx)
sinx) cos2x+
cos2x+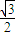 sinxcosx=
sinxcosx= (1+cos2x)+
(1+cos2x)+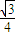 sin2x=
sin2x= cos(2x-
cos(2x-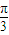 )+
)+ ,
, ,化為
,化為 cos(2x-
cos(2x-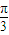 )+
)+ <
< ,即cos(2x-
,即cos(2x-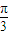 )<0,
)<0,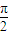 <2x-
<2x-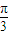 <2kπ+
<2kπ+ (k∈Z),
(k∈Z),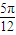 <x<kπ+
<x<kπ+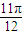 (k∈Z),
(k∈Z), 成立的x取值集合為{x|kπ+
成立的x取值集合為{x|kπ+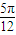 ,kπ+
,kπ+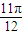 (k∈Z)}.
(k∈Z)}.

科目:高中數學 來源:2010年浙江省溫州市蒼南縣龍港高中高考數學仿真模擬試卷(文科)(解析版) 題型:解答題

 的值;
的值; 對稱,且t∈(0,π),求t的值.
對稱,且t∈(0,π),求t的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com